
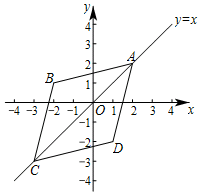
 ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Čē¹ūµćA£¬µćCĪŖijøöĮāŠĪµÄŅ»×é¶Ō½ĒµÄ¶„µć£¬ĒŅµćA£¬CŌŚÖ±Ļßy=xÉĻ£¬ÄĒĆ“³ĘøĆĮāŠĪĪŖµćA£¬CµÄ”°¼«ŗĆĮāŠĪ”±£®ČēĶ¼ĪŖµćA£¬CµÄ”°¼«ŗĆĮāŠĪ”±µÄŅ»øöŹ¾ŅāĶ¼£®
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Čē¹ūµćA£¬µćCĪŖijøöĮāŠĪµÄŅ»×é¶Ō½ĒµÄ¶„µć£¬ĒŅµćA£¬CŌŚÖ±Ļßy=xÉĻ£¬ÄĒĆ“³ĘøĆĮāŠĪĪŖµćA£¬CµÄ”°¼«ŗĆĮāŠĪ”±£®ČēĶ¼ĪŖµćA£¬CµÄ”°¼«ŗĆĮāŠĪ”±µÄŅ»øöŹ¾ŅāĶ¼£®·ÖĪö £Ø1£©ČēĶ¼1ÖŠ£¬¹Ū²ģĶ¼ĻóæÉÖŖ£ŗF”¢GÄܹ»³ÉĪŖµćM£¬PµÄ”°¼«ŗĆĮāŠĪ”±¶„µć£®
£Ø2£©¢ŁČēĶ¼2ÖŠ£¬øł¾ŻŅŃÖŖČżµćµÄ×ų±źæÉµĆ¼«ŗĆĮāŠĪĪŖÕż·½ŠĪ£¬øł¾ŻÕż·½ŠĪĆ껿¹«Ź½æÉµĆ½į¹ū£»
¢Śøł¾ŻĮāŠĪµÄŠŌÖŹµĆ£ŗPM”ĶQN£¬ĒŅ¶Ō½ĒĻß»„ĻąĘ½·Ö£¬ÓÉĮāŠĪµÄĆ껿ĪŖ8£¬ĒŅĮāŠĪµÄĆ껿µČÓŚĮ½Ģõ¶Ō½ĒĻß»żµÄŅ»°ė£¬æɵĆQNµÄ³¤£¬Ö¤Ć÷QŌŚyÖįÉĻ£¬NŌŚxÖįÉĻ£¬æÉµĆ½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬¹Ū²ģĶ¼ĻóæÉÖŖ£ŗF”¢GÄܹ»³ÉĪŖµćM£¬PµÄ”°¼«ŗĆĮāŠĪ”±¶„µć£®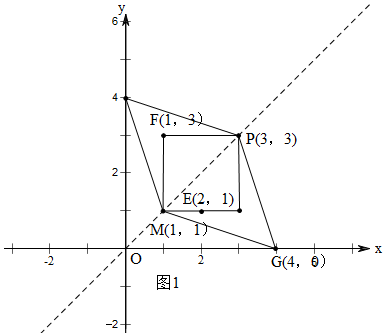
¹Ź“š°øĪŖ£ŗF£¬G£»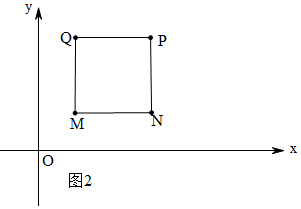
£Ø2£©¢ŁČēĶ¼2£¬”ßM£Ø1£¬1£©£¬P£Ø3£¬3£©£¬N£Ø3£¬1£©£¬
”ąMN=2£¬PN”ĶMN£¬
”ßĖıߊĪMNPQŹĒĮāŠĪ£¬
”ąĖıߊĪMNPQŹĒÕż·½ŠĪ£¬
”ąSĖıߊĪMNPQ=2”Į2=4£»
¢ŚČēĶ¼3£¬”ßµćMµÄ×ų±źĪŖ£Ø1£¬1£©£¬µćPµÄ×ų±źĪŖ£Ø3£¬3£©£¬
”ąPM=2$\sqrt{2}$£¬
”ßĖıߊĪMNPQµÄĆ껿ĪŖ8£¬
”ąSĖıߊĪMNPQ=$\frac{1}{2}$PM•QN=8£¬
¼“$\frac{1}{2}$”Į$2\sqrt{2}$”ĮQN=8£¬
”ąQN=4$\sqrt{2}$£¬
”ßĖıߊĪMNPQŹĒĮāŠĪ£¬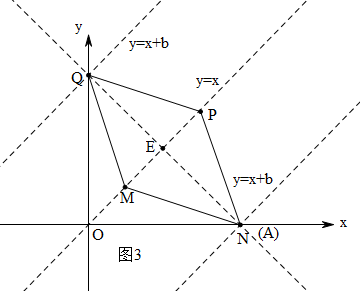
”ąQN”ĶMP£¬ME=$\sqrt{2}$£¬EN=2$\sqrt{2}$£¬
×÷Ö±ĻßQN£¬½»xÖįÓŚA£¬
”ßM£Ø1£¬1£©£¬
”ąOM=$\sqrt{2}$£¬
”ąOE=2$\sqrt{2}$£¬
”ßMŗĶPŌŚÖ±Ļßy=xÉĻ£¬
”ą”ĻMOA=45”ć£¬
”ą”÷EOAŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąEA=2$\sqrt{2}$£¬
”ąAÓėNÖŲŗĻ£¬¼“NŌŚxÖįÉĻ£¬
Ķ¬ĄķæÉÖŖ£ŗQŌŚyÖįÉĻ£¬ĒŅON=OQ=4£¬
ÓÉĢāŅāµĆ£ŗĖıߊĪMNPQÓėÖ±Ļßy=x+bÓŠ¹«¹²µćŹ±£¬bµÄȔֵ·¶Ī§ŹĒ-4”Üb”Ü4£®
µćĘĄ ±¾ĢāŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻĢā£¬æ¼²éĮĖĮāŠĪµÄŠŌÖŹ”¢Õż·½ŠĪµÄÅŠ¶Ø”¢µćM£¬PµÄ”°¼«ŗĆĮāŠĪ”±µÄ¶ØŅåµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĄķ½āĢāŅā£¬Ń§»įĄūÓĆĶ¼Ļó½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼““ŠĀĢāÄ森


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
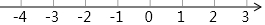
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ŅŃÖŖ¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĖüÓėxÖįµÄĮ½øö½»µć·Ö±šĪŖ£Ø-1£¬0£©£¬£Ø3£¬0£©£¬¶ŌÓŚĻĀĮŠĆüĢā£ŗ¢Łabc£¾0£»¢Ś£Øa-b£©c£¾0£»¢Ūb-c£¾0£»¢Ü4a+3b+2c£¾0£»¢Żb-2a=1£»¢Ža+b+c£¼0£»¢ß4a-2b+c£¼0£®ĘäÖŠĖłÓŠÕżČ·½įĀŪÓŠ£Ø””””£©
ŅŃÖŖ¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĖüÓėxÖįµÄĮ½øö½»µć·Ö±šĪŖ£Ø-1£¬0£©£¬£Ø3£¬0£©£¬¶ŌÓŚĻĀĮŠĆüĢā£ŗ¢Łabc£¾0£»¢Ś£Øa-b£©c£¾0£»¢Ūb-c£¾0£»¢Ü4a+3b+2c£¾0£»¢Żb-2a=1£»¢Ža+b+c£¼0£»¢ß4a-2b+c£¼0£®ĘäÖŠĖłÓŠÕżČ·½įĀŪÓŠ£Ø””””£©| A£® | 1øö | B£® | 2øö | C£® | 3øö | D£® | 4øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
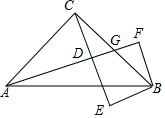 ŌŚÖ±½Ē”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=BC£¬¹żAµćµÄÖ±Ļß½»BCÓŚG£¬CD”ĶAGÓŚD£¬¹żB×÷BE”ĶCD½»CDµÄŃÓ³¤ĻßÓŚE£®
ŌŚÖ±½Ē”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=BC£¬¹żAµćµÄÖ±Ļß½»BCÓŚG£¬CD”ĶAGÓŚD£¬¹żB×÷BE”ĶCD½»CDµÄŃÓ³¤ĻßÓŚE£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com