
 如图,有一圆经过△ABC的三个顶点,且线段BC的垂直平分线与圆弧$\widehat{AC}$相交于D点,连结CD、AD,若∠B=74°,∠ACB=52°,则∠BAD=117°.
如图,有一圆经过△ABC的三个顶点,且线段BC的垂直平分线与圆弧$\widehat{AC}$相交于D点,连结CD、AD,若∠B=74°,∠ACB=52°,则∠BAD=117°. 分析 连接BD,根据DE是线段BC的垂直平分线的性质得出BD=CD,证出$\widehat{BD}=\widehat{CD}$,求出$\widehat{AC}$的度数=148°,$\widehat{AB}$的度数=104°,求出$\widehat{AD}$的度数=22°,由圆周角定理得出∠ACD=11°,求出∠BCD的度数,再由圆内接四边形的对角互补即可得出结果.
解答 解:连接BD,如图所示: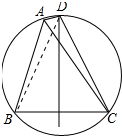
∵DE是线段BC的垂直平分线,
∴BD=CD,
∴$\widehat{BD}=\widehat{CD}$,
∵∠B=74°,∠ACB=52°,
∴$\widehat{AC}$的度数=2×74°=148°,$\widehat{AB}$的度数=2×52°=104°,
∴2$\widehat{AD}$的度数=$\widehat{AC}$的度数-$\widehat{AB}$的度数=44°,
∴$\widehat{AD}$的度数=22°,
∴∠ACD=$\frac{1}{2}$×22°=11°,
∴∠BCD=52°+11°=63°,
∴∠BAD=180°-∠BCD=117°;
故答案为:117°.
点评 本题考查的是圆周角定理、圆心角、弧、弦的关系、线段垂直平分线的性质、圆内接四边形的性质;熟练掌握圆周角定理,求出∠BCD的度数是解决问题的关键.


科目:初中数学 来源: 题型:选择题
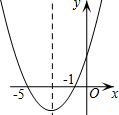 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )
如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b5•b5=2b5 | B. | (an-1)3=a3n-1 | C. | a+2a2=3a3 | D. | (a-b)5(b-a)4=(a-b)9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 写作能力 | 普通话水平 | 计算机水平 | |
| 小亮 | 90分 | 75分 | 51分 |
| 小丽 | 60分 | 84分 | 72分 |
| A. | 小丽增加多 | B. | 小亮增加多 | ||
| C. | 两人成绩不变化 | D. | 变化情况无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com