
【题目】如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是 . 
【答案】5+ ![]()
【解析】解:连接CD; ∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE与△CFD中,  ,
,
∴△ADE≌△CDF(SAS);
∴ED=DF,∠CDF=∠EDA;
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形,
∵∠C=90°,AC=BC=5,
∴AB=5 ![]() ,
,
∴当,△CEF周长的最小时,EF取最小值,
∴E、F分别为AC、BC中点时,EF的值最小,
∴EF= ![]() AB=
AB= ![]() ,
,
∴△CEF周长的最小值=CE+CF+EF=AE+CE+EF=AC+EF=5+ ![]() ;
;
所以答案是:5+ ![]() .
.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】计算
(1)27﹣19+(﹣7)﹣32;
(2)(﹣7)÷(﹣ ![]() )×(﹣
)×(﹣ ![]() );
);
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣36)
)×(﹣36)
(4)﹣14﹣ ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
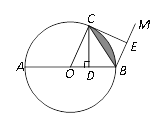
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D, 过点B作BM∥OC,在射线BM上取点E, 使BE=BD,连接CE.
(1) 当∠COB=60° 时,直接写出阴影部分的面积;
(2) 求证:CE是 ⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
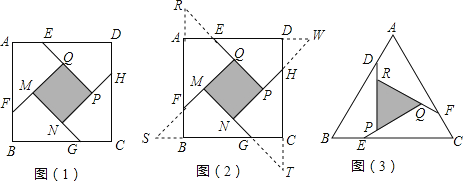
小明遇到这样一个问题:如图1,在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠GHN=∠DEP=45°时,求正方形MNPQ的面积.
小明发现,分别延长QE,MF,NG,PH交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2) .
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠),则这个新正方形的边为 ;
(2)求正方形MNPQ的面积.
(3)参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ.若S△RPQ=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
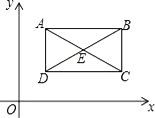
【题目】如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=![]() x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△ABD的面积是4.求证:四边形ABCD是矩形.
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△ABD的面积是4.求证:四边形ABCD是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com