
【题目】如图,在一斜坡坡顶![]() 处的同一水平线上有一古塔,为测量塔高
处的同一水平线上有一古塔,为测量塔高![]() ,数学老师带领同学在坡脚
,数学老师带领同学在坡脚![]() 处测得斜坡的坡角为
处测得斜坡的坡角为![]() ,且
,且![]() ,塔顶
,塔顶![]() 处的仰角为
处的仰角为![]() ,他们沿着斜坡攀行了
,他们沿着斜坡攀行了![]() 米,到达坡顶
米,到达坡顶![]() 处,在
处,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .
.
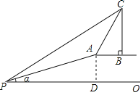
(1)求斜坡的高度![]() ;
;
(2)求塔高![]() .
.
【答案】(1)14米;(2)塔的高度为![]() 米.
米.
【解析】
(1)在Rt△APD中,根据tanα的值设AD=7k,PD=24k,利用勾股定理表示出AP,根据AP=50,求出k的值,继而可求得AD的长度;
(2)延长CB交PO于点E,设塔高为x,在Rt△CBA中,求出AB的长度,然后在Rt△PCE中,根据∠CPE=30°,利用三角函数求解.
(1)在Rt△APD中,
∵tanα=![]() ,
,
∴设AD=7k,PD=24k,
∴PA=![]() =25k,
=25k,
∵PA=50,
∴AD=APsinα=50×![]() =14(m);
=14(m);
(2)延长CB交PO于点E,可得四边形ABED为矩形,

设塔高为x,
在Rt△CBA中,
∵∠CAB=60°,tan60°=![]() ,
,
∴AB=![]() ,
,
在Rt△CPE中,
∵∠CPE=30°,
∴![]() =tan30°,
=tan30°,
即![]() ,
,
解得:x=24![]() -21.
-21.
答:塔的高度为![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距![]() km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市区九年级学生每天的健身活动情况,随机从市区九年级的12000名学生中抽取了500名学生,对这些学生每天的健身活动时间进行统计整理,作出了如下不完整的统计图(每组数据含最小值不含最大值,统计数据全部为整数),请根据以下信息解答如下问题:
时间/分 | 频数 | 频率 |
30~40 | 25 | 0.05 |
40~50 | 50 | 0.10 |
50~60 | 75 | b |
60~70 | a | 0.40 |
70~80 | 150 | 0.30 |
(1)a=_______,b=_______;
(2)请补全频数分布直方图;
(3)学生每天健身时间的中位数会落在哪个时间段?
(4)若每天健身时间在60分钟以上为符合每天“阳光一小时”的规定,则符合规定的学生人数大约是多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF于点F.
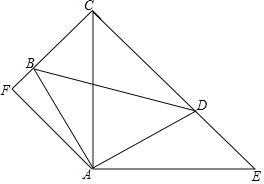
(1)求证:△ABC≌△ADE;
(2)已知BF的长为2,DE的长为6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产![]() 、
、![]() 两种机械设备,每台
两种机械设备,每台![]() 种设备的成本是
种设备的成本是![]() 种设备的1.5倍,公司若投入16万元生产
种设备的1.5倍,公司若投入16万元生产![]() 种设备,36万元生产
种设备,36万元生产![]() 种设备,则可生产两种设备共10台,请解答下列问题:
种设备,则可生产两种设备共10台,请解答下列问题:
(1)![]() 、
、![]() 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?
(2)![]() 、
、![]() 两种设备每台的售价分别是6万元、10万元,且该公司生产两种设备各30台,现公司决定对两种设备优惠出售,
两种设备每台的售价分别是6万元、10万元,且该公司生产两种设备各30台,现公司决定对两种设备优惠出售,![]() 种设备按原来售价8折出售,B种设备在原来售价的基础上优惠10%,若设备全部售出,该公司一共获利多少万元?
种设备按原来售价8折出售,B种设备在原来售价的基础上优惠10%,若设备全部售出,该公司一共获利多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
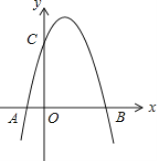
【题目】如图,二次函数![]() 的图象与x轴的一个交点为
的图象与x轴的一个交点为![]() ,另一个交点为A,且与y轴相交于C点
,另一个交点为A,且与y轴相交于C点
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由
(3)P为抛物线上一点,它关于直线BC的对称点为Q,当四边形PBQC为菱形时,求点P的坐标(直接写出答案);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,长方形OABC,点A,C分别在x轴,y轴的正半轴上,点B(6,3),现将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P.则点P的坐标为( )
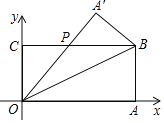
A.(![]() ,3)B.(
,3)B.(![]() ,3)C.(
,3)C.(![]() ,3)D.(
,3)D.(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com