
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ��x�ύ�ڵ�A(-4,0)��B(6,0�����㣬��y�ύ�ڵ�C��
��x�ύ�ڵ�A(-4,0)��B(6,0�����㣬��y�ύ�ڵ�C��
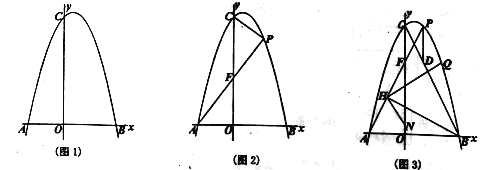
(1)��ͼl���������ߵĽ���ʽ��
(2)��ͼ2����PΪ��һ������������һ�㣬����PC��PA��PA��y���ڵ�F�����P�ĺ�����Ϊt����CPF�����ΪS����S��t�ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
(3)��ͼ3����(2)�������£�����BC������P��PD//y���BC�ڵ�D����HΪAF�е㣬�ҵ�N(0��1)������NH��BH������NHB�Ƶ�H��ʱ����ת��ʹ�ǵ�һ����H��������HF��,��һ����HN���������ڵ�Q����BH=BDʱ�����Q���꣮
���𰸡���1�������ߵĽ���ʽΪ![]() ��
��
��2��S��t�ĺ�����ϵʽΪ![]() ��
��
��3����Q������4��8��.
�������������������1��ֱ���ô��뷨�����Ľ���ʽ����2������P��PR��y�ᣬ��y���ڵ�R������P��PL��AB�ڵ�L�����P(t, ![]() )����Rt��PAL�У���ΪPL=
)����Rt��PAL�У���ΪPL=![]() AL=
AL= ![]() ������tan��PAL=
������tan��PAL=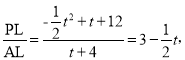 ��Rt��FAO������tan��FAO=
��Rt��FAO������tan��FAO= ![]() , ����OF=12-2t������CF=CO- OF=12-��12-2t��=2t������
, ����OF=12-2t������CF=CO- OF=12-��12-2t��=2t������![]() ����3���ӳ�PD��x���ڵ�L��ȡOA���е�K������HK,����H��HG��y���ڵ�G��OF��12-2t��HΪAF���е� HK ��OA ������HK=
����3���ӳ�PD��x���ڵ�L��ȡOA���е�K������HK,����H��HG��y���ڵ�G��OF��12-2t��HΪAF���е� HK ��OA ������HK=![]() 6-t=BL����ΪHK=BL BH=BD �����ԡ�BHK�ա�DBL ������BK=DL=8��ֱ��BC�Ľ���ʽΪ
6-t=BL����ΪHK=BL BH=BD �����ԡ�BHK�ա�DBL ������BK=DL=8��ֱ��BC�Ľ���ʽΪ![]() ���D
���D![]() ��DL=12-2t =8 t=2 �����Ե�P��2��12�������H��-2��4����tan��AHK=tan��HBK=
��DL=12-2t =8 t=2 �����Ե�P��2��12�������H��-2��4����tan��AHK=tan��HBK=![]() �����ԡ�AHK=��HBK �����AHB=90��������Ϊ��NHB=��PHQ �����ԡ�NHQ=90��������Q��QM��HG�ڵ�M�����ԡ�HNG=��QHM ������Ϊ��N��0��1����HG=2������GN=3��tan��HNG=tan��QHM =
�����ԡ�AHK=��HBK �����AHB=90��������Ϊ��NHB=��PHQ �����ԡ�NHQ=90��������Q��QM��HG�ڵ�M�����ԡ�HNG=��QHM ������Ϊ��N��0��1����HG=2������GN=3��tan��HNG=tan��QHM =![]() ��
�� ![]() �����Q(
�����Q(![]() ,
,![]() ) ����QM=
) ����QM=![]() -4=
-4=![]() ������HM=
������HM= ![]() +2 ������
+2 ������  ����ã�
����ã� ![]() ������ ���Q��4��8����
������ ���Q��4��8����
���������
��1�����������![]() ����A��-4��0����B��6��0��
����A��-4��0����B��6��0��
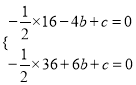 ���
���![]()
�������߽���ʽΪ![]()
��2������P��PR��y�ᣬ��y���ڵ�R������P��PL��AB�ڵ�L����ͼ��ʾ��
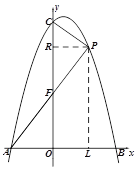
���P(t, ![]() )����Rt��PAL��
)����Rt��PAL��
��PL=![]() AL=
AL= ![]()
��tan��PAL= 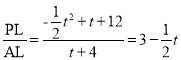
��Rt��FAO��
��tan��FAO= ![]() ,
,
��OF=12-2t
��CF=CO- OF=12-��12-2t��=2t
��![]()
��3���ӳ�PD��x���ڵ�L��ȡOA���е�K������HK,����H��HG��y���ڵ�G����ͼ��ʾ��
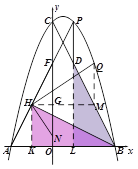
OF��12-2t��HΪAF���е� HK ��OA
��HK=![]() 6-t=BL
6-t=BL
��HK=BL BH=BD
���BHK�ա�DBL
��BK=DL=8
ֱ��BC�Ľ���ʽΪ![]() ����
����
���D![]()
DL=12-2t =8 t=2
���P��2��12��
���H��-2��4��
tan��AHK=tan��HBK=
���AHK=��HBK
���AHB=90��
�ߡ�NHB=��PHQ
���NHQ=90����
����Q��QM��HG�ڵ�M��
���HNG=��QHM
�ߵ�N��0��1����HG=2��
��GN=3��tan��HNG=tan��QHM =![]() ��
�� ![]()
���Q(![]() ,
,![]() )
)
QM=![]() -4=
-4=![]()
HM= ![]() +2
+2
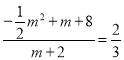 ��
��
![]()
���Q��4��8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵꽫ij�ַ�װ���ɱ������40%���ۣ�����8���Ż����������ÿ������װ�Կɻ���15Ԫ�������ַ�װÿ���ijɱ��ǣ���
A. 120Ԫ B. 125Ԫ C. 135Ԫ D. 140Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��B=30�㣬��AB�Ĵ�ֱƽ����DE��AB�ڵ�E����BC�ڵ�D��CD=3����BC�ij�Ϊ�� �� 
A.6
B.9
C.10
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=AC��D��AB��һ�㣬DE��BC�ڵ�E��ED���ӳ��߽�CA���ӳ����ڵ�F����֤����ADF�ǵ��������Σ� 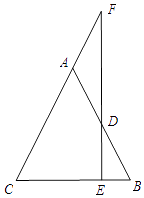
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ����һ�����Ϊ200ƽ���ľ��λ��ԣ����ij��ȿ���10�ף��軨�ԵĿ�Ϊx�ף�����з���Ϊ���� ��
A. x��x-10��=200 B. 2x+2��x-10��=200
C. x��x+10��=200 D. 2x+2��x+10��=200
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DE�DZ�AB�Ĵ�ֱƽ���ߣ���AB��E����AC��D������BD�� 
��1������ABC=��C����A=40�㣬���DBC�Ķ�����
��2����AB=AC���ҡ�BCD���ܳ�Ϊ18cm����ABC���ܳ�Ϊ30cm����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC�У�AC=BC����ACB=90�㣬��D��AB���е㣬��E��AB����һ�㣮
��1����ͼ�٣�BF��ֱCE�ڵ�F����CD�ڵ�G����˵��AE=CG�� 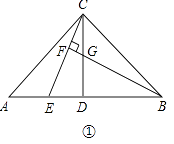
��2����ͼ�ڣ���AH��ֱ��CE���ӳ��ߣ�����ΪH����CD���ӳ����ڵ�M����ͼ����BE��ȵ��߶��� �� ��˵�����ɣ� 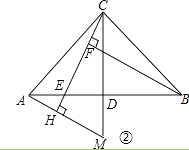
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��22+����4��+����2��+4
��2������ ![]() +1
+1 ![]() ��
�� ![]() ��������24��
��������24��
��3��3��6�£���2����|�� ![]() |
|
��4��2a����3b��a��+b
��5��3��x2��y2��+��y2��z2����2��z2��y2��
��6������ ![]() ��������4��2��0.25������5��������4��3 ��
��������4��2��0.25������5��������4��3 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һֻ�׳���5��5�ķ���ÿС��߳�Ϊ1���������������˶�������A����������B��C��D���������׳森�涨������������Ϊ��������������Ϊ���������A��B��Ϊ��A��B��+1��+4������B��A��Ϊ��B��A����1����4�������е�һ����ʾ���ҷ��ڶ�������ʾ���·�����ôͼ�� 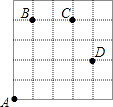
��1��A��C�� �� ����B��D�� �� ����
��2������ֻ�׳������·��ΪA��B��C��D�������ü׳��߹���·�̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com