
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | ${({-\frac{1}{2}x{y^2}})^3}=-\frac{1}{6}{x^3}{y^6}$ | ||
| C. | (-x)5÷(-x)2=x3 | D. | $\sqrt{18}+\root{3}{-64}=3\sqrt{2}-4$ |
分析 根据二次根式的加减,积的乘方等于乘方的积,同底数幂的除法底数不变指数相减,实数的运算,可得答案.
解答 解:A、$\sqrt{2}$、$\sqrt{3}$不是同类项,不能合并,故选项A错误;
B、${(-\frac{1}{2}x{y^2})^3}={(-\frac{1}{2})^3}{x^3}{({y^2})^3}=-\frac{1}{8}{x^3}{y^6}$,故选项B错误;
C、(-x)5÷(-x)2=(-x)5-2=(-x)3=-x3,故选项C错误;
D、$\sqrt{18}+\root{3}{-64}=3\sqrt{2}+(-4)=3\sqrt{2}-4$,故选项D正确.
故选:D.
点评 本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
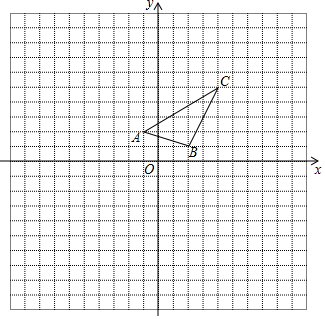 如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2)、B(2,1)、C(4,5).
如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2)、B(2,1)、C(4,5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
| A. | 5 | B. | -3 | C. | -13 | D. | -27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com