
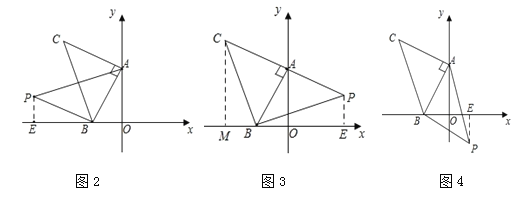
【题目】如图,平面直角坐标系中有点B(-2,0)和y轴上的动点A(0,a),其中a>0,以点A为直角顶点在第二象限内作等腰直角三角形ABC,设点C的坐标为(c,d).
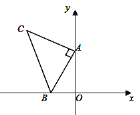
(1)当a=4时,则点C的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=4时,在坐标平面内是否存在点P(不与点C重合),使△PAB与△ABC全等?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)﹣4,6;(2)c+d=2的值不变,值为2;(3)(﹣6,2)或(4,2)或(2,﹣2).
【解析】
(1)先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=4,AE=BO=2,即可得出点C的坐标;
(2)先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=a,AE=BO=2,可得OE=a+2,即可得出点C的坐标为(﹣a,a+2),据此可得c+d的值不变;
(3)分为三种情况讨论,分别画出符合条件的图形,构造直角三角形,证出三角形全等,根据全等三角形对应边相等即可得出答案.
(1)如图1,过点C作CE⊥y轴于E,则∠CEA=∠AOB.
∵△ABC是等腰直角三角形,∴AC=BA,∠BAC=90°,∴∠ACE+∠CAE=90°=∠BAO+∠CAE,∴∠ACE=∠BAO.
在△ACE和△BAO中,∵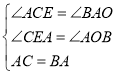 ,∴△ACE≌△BAO(AAS),∴BO=AE,AO=CE.
,∴△ACE≌△BAO(AAS),∴BO=AE,AO=CE.
∵B(﹣2,0),A(0,4),∴BO=AE=2,AO=CE=4,∴OE=4+2=6,∴C(﹣4,6).
故答案为:﹣4,6;

(2)动点A在运动的过程中,c+d=2的值不变,值为2.证明如下:
如图1,过点C作CE⊥y轴于E,则∠CEA=∠AOB.
∵△ABC是等腰直角三角形,∴AC=BA,∠BAC=90°,∴∠ACE+∠CAE=90°=∠BAO+∠CAE,∴∠ACE=∠BAO.
在△ACE和△BAO中,∵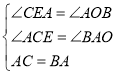 ,∴△ACE≌△BAO(AAS),∴BO=AE,AO=CE.
,∴△ACE≌△BAO(AAS),∴BO=AE,AO=CE.
∵B(﹣2,0),A(0,a),∴BO=AE=2,AO=CE=a,∴OE=2+a,∴C(﹣a,2+a).
又∵点C的坐标为(c,d),∴c+d=﹣a+2+a=2,即c+d=2,值不变;
(3)存在一点P,使△PAB与△ABC全等,分为三种情况:
①如图2,过P作PE⊥x轴于E,则∠PBA=∠AOB=∠PEB=90°,∴∠EPB+∠PBE=90°,∠PBE+∠ABO=90°,∴∠EPB=∠ABO.
在△PEB和△BOA中,∵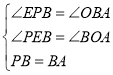 ,∴△PEB≌△BOA(AAS),∴PE=BO=2,EB=AO=4,∴OE=2+4=6,即P的坐标是(﹣6,2);
,∴△PEB≌△BOA(AAS),∴PE=BO=2,EB=AO=4,∴OE=2+4=6,即P的坐标是(﹣6,2);
②如图3,过C作CM⊥x轴于M,过P作PE⊥x轴于E,则∠CMB=∠PEB=90°.
∵△CAB≌△PAB,∴∠PBA=∠CBA=45°,BC=BP,∴∠CBP=90°,∴∠MCB+∠CBM=90°,∠CBM+∠PBE=90°,∴∠MCB=∠PBE.
在△CMB和△BEP中,∵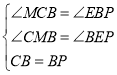 ,∴△CMB≌△BEP(AAS),∴PE=BM,CM=BE.
,∴△CMB≌△BEP(AAS),∴PE=BM,CM=BE.
∵C(﹣4,6),B(﹣2,0),∴PE=2,OE=BE﹣BO=6﹣2=4,即P的坐标是(4,2);
③如图4,过P作PE⊥x轴于E,则∠BEP=∠AOB=90°.
∵△CAB≌△PBA,∴AB=BP,∠CAB=∠ABP=90°,∴∠ABO+∠PBE=90°,∠PBE+∠BPE=90°,∴∠ABO=∠BPE.
在△BOA和△PEB中,∵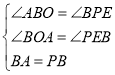 ,∴△BOA≌△PEB(AAS),∴PE=BO=2,BE=OA=4,∴OE=BE﹣BO=4﹣2=2,即P的坐标是(2,﹣2).
,∴△BOA≌△PEB(AAS),∴PE=BO=2,BE=OA=4,∴OE=BE﹣BO=4﹣2=2,即P的坐标是(2,﹣2).
综合上述:符合条件的P的坐标是(﹣6,2)或(4,2)或(2,﹣2).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD.过E作EF∥DC交BC的延长线于F.
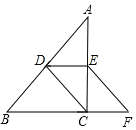
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是18cm,AC的长为6cm,求线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
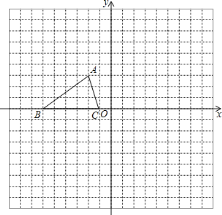
【题目】(1)直接写出A点关于y轴对称的点的坐标是______.
(2)将△ABC向右平移六个单位后得△A1B1C1,则线段AB平移扫过的面积是______.
(3)作出△A1B1C1关于x轴对称的图形△A2B2C2,画出△A2B2C2,连接A2B交y轴于点D,直接写出D点的坐标______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在一条直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
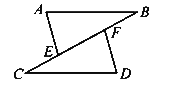
(1)求证:AB=CD;
(2)若AB=CF,∠B=50°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
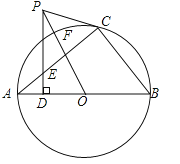
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com