练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E，连结OD、OE，若∠A=65°，则∠DOE=　　．


    50°          解：如图，连接BE．

    ∵BC为⊙O的直径，

    ∴∠CEB=∠AEB=90°，

    ∵∠A=65°，

    ∴∠ABE=25°，

    ∴∠DOE=2∠ABE=50°，（圆周角定理）

    故答案为：50°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    等腰三角形一腰上的高与另一腰的夹角为36°，则该等腰三角形的底角的度数为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC∽△CBD，CD=2，AC=3，BC=4，那么AB的值等于（　　）

    A．  5             B．6             C  7             D． 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线点F．问：

    （1）图中△APD与哪个三角形全等？并说明理由；

    （2）求证：△APE∽△FPA；

    （3）猜想：线段PC，PE，PF之间存在什么关系？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，半径为3的⊙O内有一点A，OA=，点P在⊙O上，当∠OPA最大时，PA的长等于（　　）

    A．             B．           C3 D．           2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


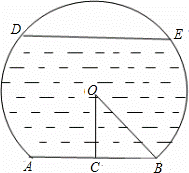
    一个弓形桥洞截面示意图如图所示，圆心为O，弦AB是水底线，OC⊥AB，AB=24m，sin∠COB=，DE是水位线，DE∥AB．

    （1）当水位线DE=4m时，求此时的水深；

    （2）若水位线以一定的速度下降，当水深8m时，求此时∠ACD的余切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，PA，PB分别与⊙O相切于点A，B，∠APB=60°，连接AO，BO．

    （1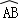）所对的圆心角∠AOB=　 　；

    （2）求证：PA=PB；

    （3）若OA=3，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD．若∠A=25°，则∠C=　　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


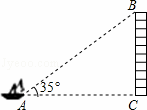
    如图，从一般船的点A处观测海岸上高为41m的灯塔BC（观测点A与灯塔底部C在一个水平面上），测得灯塔顶部B的仰角为35°，则观测点A到灯塔BC的距离约为　　m（精确到1m）．

    （参考数据：sin35°≈0.6，cos35°≈0.8，tan35°≈0.7）

    查看答案和解析>>

    同步练习册答案