
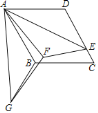
【题目】如图,在菱形ABCD中,![]() ,点E在边CD上,且
,点E在边CD上,且![]() ,
,![]() 与
与![]() 关于AE所在的直线成对称图形
关于AE所在的直线成对称图形![]() 以点A为中心,把
以点A为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接GF,则线段GF的长为______.
,连接GF,则线段GF的长为______.
【答案】![]()
【解析】
连接BE,作BH⊥CD于H,先证△BAE≌△FAG,得到BE=GF,在Rt△BCH中,由∠C=60°得出CH=4,BH2=48,再在Rt△BEH中,利用勾股定理即可求出BE的长即可得解.
解:如图,连接BE,作BH⊥CD于H,则∠BHC=90°,
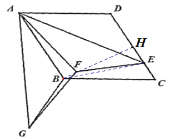
由题意可知,菱形ABCD中,AB=BC=CD=AD=8,DE=6,∠C=∠DAB,
由旋转知识可知,∠DAB=60°,AE=AG,∠DAE=∠BAG,
由对称知识可知,AD=AF,∠DAE=∠FAE,
∴∠C=∠DAB=60°,EC=CD-DE=8-6=2,AB=AF,∠FAE=∠BAG,
∴∠FAE+∠BAF=∠BAG+∠BAF,即∠BAE=∠FAG,
∴△BAE≌△FAG,
∴BE=GF,
∵∠BHC=90°,∠C=60°,
∴CH=BC·cos60°=8×![]() =4,
=4,
∴HE=CH-CE=4-2=2,BH2=BC2-CH2=82-42=48,
∴GF=BE=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )
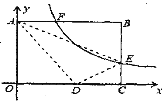
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G,
(1)如图1,求证:CF=BG;
(2)如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
求证:PB=CP+CF;
(3)如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3![]() ,BG=6,求AC的长.
,BG=6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多![]() 元,用
元,用![]() 元购得的排球数量与用
元购得的排球数量与用![]() 元购得的足球数量相等.
元购得的足球数量相等.
⑴排球和足球的单价各是多少元?
⑵若恰好用去![]() 元,有哪几种购买方案?
元,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有__________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )
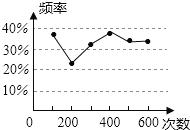
A.从一装有2个白球和1个红球的袋子中任取一球,取到红球的概率
B.掷一枚正六面体的骰子,出现1点的概率
C.抛一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为![]() .其中正确的结论有( )
.其中正确的结论有( )
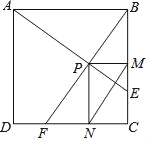
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的三个顶点的坐标分别为A(-3,2)、B(0,4)、C(0,2).
⑴将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C.平移△ABC,若A对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
⑵若将△A1B1C绕某一点旋转得到△A2B2C2,请直接写出旋转中心的坐标为 .
⑶在x轴上找一点P,使得直线CP将△ABC的面积分为1:2,直接写出P点的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com