
【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。
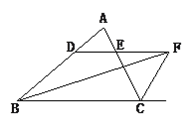
(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
【答案】(1)详见解析;(2)BD=DE+CE;(3)60.
【解析】试题分析:(1)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(2)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE;
(3)作BF边上的高,由勾股定理得到高为5,计算得到△BDF的面积为60.
试题解析:(1)△DBF、△ECF
以说明△DBF为例:
∵BF平分∠ABC
∴∠DBF=∠CBF
∵DF∥BC
∴∠CBF=∠DFB
∴∠DBF=∠DFB,
即△DBF为等腰三角形;
(2)存在:BDCE=DE,
证明:∵DF=BD,CE=EF,
∴BDCE=FDEF=DE.
(3)作DM⊥BF与点M,
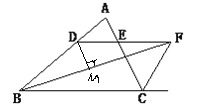
由(1)知△DBF为等腰三角形,
∴BM=![]() BF=12cm,
BF=12cm,
由(2)知BD=DE+EC=5+8=13cm,
由勾股定理,得DM=![]() =5cm,
=5cm,
S△BDF=![]() ×BF×DM=
×BF×DM=![]() ×24×5= 60(cm2)
×24×5= 60(cm2)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
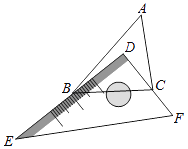
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
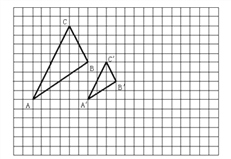
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B'C'的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点 O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.

(1)求证:PC=PG;
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为![]() 时,求弦ED的长.
时,求弦ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交与点P,若∠CAP=50°,则∠BPC的度是( )

A. 80° B. 60° C. 50° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com