
【题目】如图,△ABC是⊙O的内接三角形,直径AB=10.sinA=![]() ,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
(1)当DF经过圆心O时,求AD的长;
(2)求证:△ACF∽△ABD;
(3)求CFDH的最大值.

【答案】(1)![]() (2)证明见解析(3)当x=4时,CFDH的最大值为
(2)证明见解析(3)当x=4时,CFDH的最大值为![]()
【解析】
(1)由AB是直径知∠ACB=90°,依据三角函数求出BC=6,由勾股定理求出AC=8,由AB⊥DE知∠AFD=∠ACB=90°,结合∠A为公共角可证△ADF∽△ABC,得出对应边成比例,即可求出AD的长;
(2)由△ADF∽△ABC知![]() ,结合∠A为△ACF和△ABD的公共角可证△ACF∽△ABD;
,结合∠A为△ACF和△ABD的公共角可证△ACF∽△ABD;
(3)连接CH,先证△ACH∽△HCD得出比例式,即CFDH=CDAF,再设AD=x,则CD=8﹣x,AF=![]() x,从而得出CFDH=﹣
x,从而得出CFDH=﹣![]() (x﹣4)2+
(x﹣4)2+![]() ,利用二次函数的性质求解可得.
,利用二次函数的性质求解可得.
(1)当DF经过圆心O时,AF=OA=5,
∵AB为直径,AB=10,
∴∠ACB=90°,
∴sinA=![]() ,
,
∴BC=6,
由勾股定理得:![]() ,
,
∵AB⊥DE,
∴∠AFD=∠ACB=90°,
∵∠A=∠A,
∴△ADF∽△ABC,
∴![]() ,
,
∴![]() ;
;
(2)证明:由(1)得:△ADF∽△ABC,
∴![]() ,即
,即![]() ,
,
又∵∠A为△ACF和△ABD的公共角,
∴△ACF∽△ABD;
(3)连接CH,如图所示:
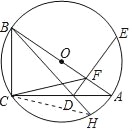
由(2)知△ACF∽△ABD,
∴∠ABD=∠ACF,
∵∠ABD=∠ACH,
∴∠ACH=∠ACF,
又∵∠CAF=∠H,
∴△ACH∽△HCD,
∴![]() ,即CFDH=CDAF,
,即CFDH=CDAF,
设AD=x,则CD=8﹣x,AF=![]() x,
x,
∴CFDH=![]() x(8﹣x)=﹣
x(8﹣x)=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣4)2+
(x﹣4)2+![]() ,
,
∴当x=4时,CFDH的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
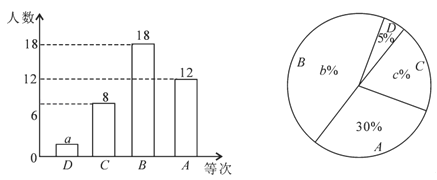
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
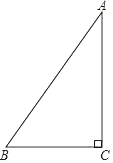
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);
(2)在(1)作出的图形中,若∠A=30°,BC=![]() ,则点D到AB的距离等于 .
,则点D到AB的距离等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.
(1)求第一次每个足球的进价是多少元?
(2)若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购进甲、乙两种规格的书架,经市场调查发现有线上和线下两种购买方式,具体情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在线下购买甲、乙两种书架共30个,花费8280元,求甲、乙两种书架各购买了多少个?
(2)如果在线上购买甲、乙两种书架共30个,且购买乙种书架的数量不少于甲种书架的3倍,请求出花费最少的购买方案及花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
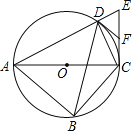
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
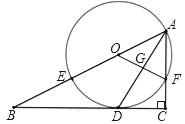
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AD边的中点.
(1)用直尺和圆规作⊙O,使⊙O 经过B、C、E三点;(要求:尺规作图,保留作图痕迹,不写作法);
(2)若正方形的边长为4,求(1)中所作⊙O的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com