
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
探究:①观察操作结果,哪一个三角形与△BPC相似,写出你的结论,(找出两对即可);并选择其中一组说明理由;
②当点P位于CD的中点时,直接写出① 中找到的两对相似三角形的相似比和面积比.

分两种情况:
①如图(1),
∵∠BPE=90°,
∴∠BPC+∠DPE=90°,又∠BPC+∠PBC=90°,
∴∠PBC=∠DPE,又∠C=∠D=90°,
∴△BPC∽△PED.
如图(2),同理可证△BPC∽△BEP∽△PCE.
②如图(1),∵△BPC∽△PED,
∴△PED与△BPC的周长比等于对应边的比,即PD与BC的比,
∵点P位于CD的中点,
∴PD与BC的比为1:2,
∴△PED与△BPC的周长比1:2,
△PED与△BPC的面积比1:4
如图(2),∵△BPC∽△BEP,
∴△BEP与△BPC的周长比等于对应边的比,即BP与BC的比,
∵点P位于CD的中点,
设BC=2k,则PC=k,BP=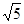 k,
k,
∴BP与BC的比为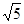 :2,
:2,
△BEP与△BPC的周长比为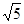 :2,△BEP与△BPC的面积比为5:4.
:2,△BEP与△BPC的面积比为5:4.
同理:△PCE∽△BPC,周长比1:2,面积比1:4.
【解析】由于本题直角三角形的摆放方法没有确定,因此要分两种情况进行讨论:
①直角三角形的斜边与AD相交;(如图1)
②直角三角形的斜边与BC边在同一条直线上(如图2);解题思路一致.
以①为例说明:△DEP和△BCP中,∠DEP和∠BPC同为∠DPE的余角,因此这两角相等,易证得两三角形相似.当P为CD中点时,PD=CP,可根据相似三角形得出的比例关系式求出DE和BC的表达式,进一步可求得两三角形的相似比和面积比.


科目:初中数学 来源: 题型:
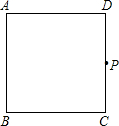 操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合(含30度角的直角三角板),并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合(含30度角的直角三角板),并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.查看答案和解析>>
科目:初中数学 来源:2012年河北省石家庄市42中学九年级第二次模拟考试数学试卷(带解析) 题型:解答题
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
探究:①观察操作结果,哪一个三角形与△BPC相似,写出你的结论,(找出两对即可);并选择其中一组说明理由;
②当点P位于CD的中点时,直接写出① 中找到的两对相似三角形的相似比和面积比.
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《图形的相似》(05)(解析版) 题型:解答题
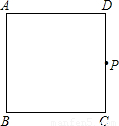
查看答案和解析>>
科目:初中数学 来源:2003年云南省昆明市中考数学试卷(解析版) 题型:解答题
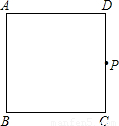
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com