
【题目】某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了 ![]() m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
【答案】
(1)解:设售价应为x元,依题意得:
2290﹣15(x﹣11)÷0.5≥2200,
解得x≤14.
答:2月份售价应不高于14元
(2)解:[14(1﹣ ![]() m%)﹣10(1+10%)]×2200(1+m%)=6600,令m%=t,
m%)﹣10(1+10%)]×2200(1+m%)=6600,令m%=t,
原式为(3﹣2t)(1+t)=3.
t1=0(不合题意,舍去),t2=0.5,
∴m=50.
答:m的值是50.
【解析】由"笔记本在2月份的销售量不低于2200本“可翻译为不等式2290﹣15(x﹣11)÷0.5≥2200;(2)“3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元”可转化为“方程[14(1﹣ 1 7 m%)﹣10(1+10%)]×2200(1+m%)=6600,解出m的值.


科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m使得关于x,y的二元一次方程组 ![]() 有解,且使关于x的分式方程
有解,且使关于x的分式方程 ![]() ﹣1=
﹣1= ![]() 有正数解,那么这五个数中所有满足条件的m的值之和是( )
有正数解,那么这五个数中所有满足条件的m的值之和是( )
A.1
B.2
C.﹣1
D.﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC 中,∠CAB=90°,AC=AB,点 D、E 是 BC 上的两点,且∠DAE=45°,△ADC 与△ADF 关于直线AD 对称.
(1)求证:△AEF≌△AEB;
(2)求∠DFE 的度数.
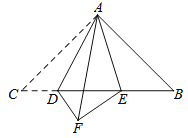
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.

(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y= ![]() (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(1)若EB= ![]() OD,求点E的坐标;
OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,其中
,其中![]() ,
,![]() ,点
,点![]() 是
是![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 是在直线
是在直线![]() 与直线
与直线![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于
于![]() ,则
,则![]() 与
与![]() 之间可满足的数量关系式为______________.
之间可满足的数量关系式为______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com