
【题目】已知线段AB=12,CD=6,线段CD在直线AB上运动(A在B的左侧,C在D的左侧).
(1)当D点与B点重合时,AC=_________;
(2)点P是线段AB延长线上任意一点,在(1)的条件下,求PA+PB–2PC的值;
(3)M、N分别是AC、BD的中点,当BC=4时,求MN的长.
![]()
【答案】(1)6;(2)PA+PB–2PC=0;(3)MN=9.
【解析】分析:(1)根据题意即可得到结论;(2)由(1)得AC=![]() AB,CD=
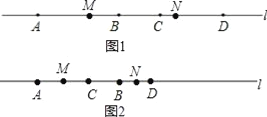
AB,CD=![]() AB,根据线段的和差即可得到结论;(3)需要分类讨论:①如图1,当点C在点B的右侧时,根据“M、N分别为线段AC、BD的中点”,先计算出AM、DN的长度,然后计算MN=AD-AM-DN;②如图2,当点C位于点B的左侧时,利用线段间的和差关系求得MN的长度.
AB,根据线段的和差即可得到结论;(3)需要分类讨论:①如图1,当点C在点B的右侧时,根据“M、N分别为线段AC、BD的中点”,先计算出AM、DN的长度,然后计算MN=AD-AM-DN;②如图2,当点C位于点B的左侧时,利用线段间的和差关系求得MN的长度.
本题解析:
(1)当D点与B点重合时,AC=AB﹣CD=6;
故答案为:6;
(2)由(1)得AC=![]() AB,
AB,
∴CD=![]() AB,
AB,
∵点P是线段AB延长线上任意一点,
∴PA+PB=AB+PB+PB,PC=CD+PB=![]() AB+PB,
AB+PB,
∴PA+PB﹣2PC=AB+PB+PB﹣2(![]() AB+PB)=0;
AB+PB)=0;
(3)如图1,∵M、N分别为线段AC、BD的中点,
∴AM=![]() AC=
AC=![]() (AB+BC)=8,
(AB+BC)=8,
DN=![]() BD=
BD=![]() (CD+BC)=5,
(CD+BC)=5,
∴MN=AD﹣AM﹣DN=9;
如图2,∵M、N分别为线段AC、BD的中点,
∴AM=![]() AC=
AC=![]() (AB﹣BC)=4,
(AB﹣BC)=4,
DN=![]() BD=
BD=![]() (CD﹣BC)=1,
(CD﹣BC)=1,
∴MN=AD﹣AM﹣DN=12+6﹣4﹣4﹣1=9.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
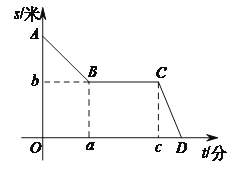
【题目】李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早穿皮袄午穿纱”这句民谣形象地描绘了我们新疆奇妙的气温变化现象.乌鲁木齐市五月的某一天,最低气温是t ℃,温差是15 ℃,则当天的最高气温是________℃.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两双曲线y=![]() 与y=﹣
与y=﹣![]() 分别位于第一、四象限,A是y轴上任意一点,B是y=﹣
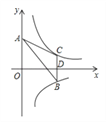
分别位于第一、四象限,A是y轴上任意一点,B是y=﹣![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣
在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣![]() );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )
A. B. C. D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
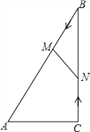
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知☉O的半径为5,且圆心O到直线l的距离是方程x2-4x-12=0的一个根,则直线l与圆的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com