
科目:初中数学 来源: 题型:解答题
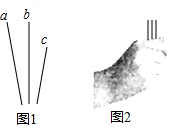 甲、乙、丙三人用三根完全相同的吸管玩游戏,将其中一根剪去一段(如图1所示),甲把三根吸管按如图2所示的方式拿在手中,使露出的部分完全相同,乙先从中抽取一根不放回,丙再从中抽取一根.
甲、乙、丙三人用三根完全相同的吸管玩游戏,将其中一根剪去一段(如图1所示),甲把三根吸管按如图2所示的方式拿在手中,使露出的部分完全相同,乙先从中抽取一根不放回,丙再从中抽取一根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
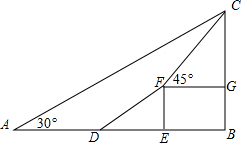 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | 11 | C. | 12 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com