
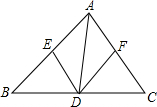
 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
分析 由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形;
如果AD⊥BC且AB=AC,那么AD平分∠BAC,同上可得四边形AEDF是菱形.
故以上答案都正确.
解答 解:由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形.故A、B正确;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形,而不一定是矩形.故C错误;
如果AD⊥BC且AB=AC,那么AD平分∠BAC,同上可得四边形AEDF是菱形.故D正确.
故选C
点评 本题考查平行四边形、矩形及菱形的判定,具体选择哪种方法需要根据已知条件来确定.


科目:初中数学 来源: 题型:选择题

| A. | ${({\frac{1}{4}})^n}$ | B. | ${({\frac{1}{4}})^{n-1}}$ | C. | ${({\frac{1}{2}})^n}$ | D. | ${({\frac{1}{2}})^{n-1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
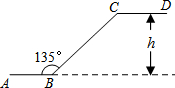 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.
如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
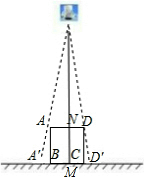 如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.
如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com