
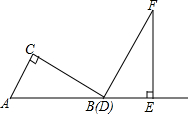
 两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).分析 (1)根据锐角三角函数,可得BG的长,根据线段的和差,可得GE的长,根据矩形的性质,可得答案;
(2)分类讨论:①当0≤t<6时,根据三角形的面积公式,可得答案;②当6≤t<12时,③当12<t≤15时,根据面积的和差,可得答案;
(3)根据点与直线上所有点的连线中垂线段最短,可得M在线段NG上,根据三角形的中位线,可得NG的长,根据锐角三角函数,可得MG的长,根据线段的和差,可得答案.
解答 解:(1)如图1所示:作CG⊥AB于G点.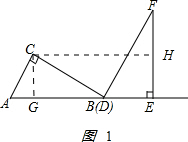 ,
,
在Rt△ABC中,由AC=6,∠ABC=30,得
BC=$\frac{AC}{tan30°}$=6$\sqrt{3}$.
在Rt△BCG中,BG=BC•cos30°=9.
四边形CGEH是矩形,
CH=GE=BG+BE=9+6=15cm,
故答案为:15;
(2)①当0≤x<6时,如图2所示.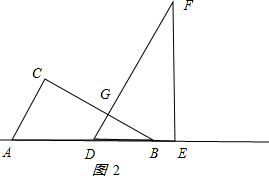 ,
,
∠GDB=60°,∠GBD=30°,DB=x,得
DG=$\frac{1}{2}$x,BG=$\frac{\sqrt{3}}{2}$x,重叠部分的面积为y=$\frac{1}{2}$DG•BG=$\frac{1}{2}$×$\frac{1}{2}$x×$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{8}$x2
②当6≤x<12时,如图3所示.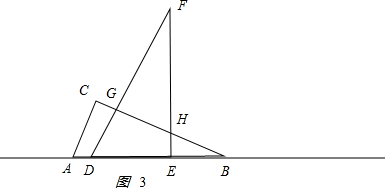 ,
,
BD=x,DG=$\frac{1}{2}$x,BG=$\frac{\sqrt{3}}{2}$x,BE=x-6,EH=$\frac{\sqrt{3}}{3}$(x-6).
重叠部分的面积为y=S△BDG-S△BEH=$\frac{1}{2}$DG•BG-$\frac{1}{2}$BE•EH,
即y=$\frac{1}{2}$×$\frac{1}{2}$x×$\frac{\sqrt{3}}{2}$x-$\frac{1}{2}$(x-6)$\frac{\sqrt{3}}{3}$(x-6)
化简,得y=-$\frac{\sqrt{3}}{24}$x2+2$\sqrt{3}$x-6$\sqrt{3}$;
③当12<x≤15时,如图4所示.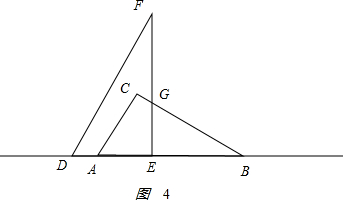 ,
,
AC=6,BC=6$\sqrt{3}$,BD=x,BE=(x-6),EG=$\frac{\sqrt{3}}{3}$(x-6),
重叠部分的面积为y=S△ABC-S△BEG=$\frac{1}{2}$AC•BC-$\frac{1}{2}$BE•EG,
即y=$\frac{1}{2}$×6×6$\sqrt{3}$-$\frac{1}{2}$(x-6)$\frac{\sqrt{3}}{3}$(x-6),
化简,得y=18$\sqrt{3}$-$\frac{\sqrt{3}}{6}$(x2-12x+36)=-$\frac{\sqrt{3}}{6}$x2+2$\sqrt{3}$x+12$\sqrt{3}$;
综上所述:y=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{8}{x}^{2}(0≤x<6)}\\{-\frac{\sqrt{3}}{24}{x}^{2}+2\sqrt{3}x-6\sqrt{3}(6≤x<12)}\\{-\frac{\sqrt{3}}{6}{x}^{2}+2\sqrt{3}x+12\sqrt{3}(12≤x≤15)}\end{array}\right.$;
(3)如图5所示作NG⊥DE于G点.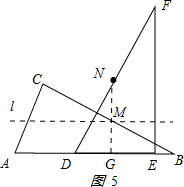 ,
,
点M在NG上时MN最短,
NG是△DEF的中位线,
NG=$\frac{1}{2}$EF=$3\sqrt{3}$.
MB=$\frac{1}{2}$CB=3$\sqrt{3}$,∠B=30°,
MG=$\frac{1}{2}$MB=$\frac{3\sqrt{3}}{2}$,
MN最小=3$\sqrt{3}$-$\frac{3\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了几何变换综合题,(1)利用了锐角三角函数,矩形的性质;(2)利用面积的和差,分类讨论时解题关键,以防遗漏;(3)利用了垂线段最短的性质,三角形的中位线定理,锐角三角函数.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
| A. | 图象过(1,2)点 | B. | 图象在第一、三象限 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
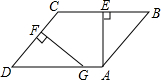 如图,在?ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.
如图,在?ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 93,96 | B. | 96,96 | C. | 96,100 | D. | 93,100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
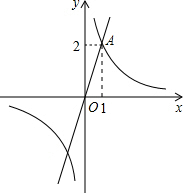 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com