
【题目】已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点,且经过A(m﹣1,n)和B(m+3,n),过点A,B分别作x轴的垂线,垂足记为M,N,则四边形AMNB的周长为 .
【答案】22
【解析】y=2x2+bx+c= ![]() ,
,
∵抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点,
∴ ![]() ,得
,得 ![]() ,
,
∵抛物线y=2x2+bx+c经过A(m﹣1,n)和B(m+3,n),
∴该抛物线的对称轴为:直线x= ![]() =
= ![]() ,
,
∴b=﹣4(m+1),
∴ ![]() =2m2+4m+1,
=2m2+4m+1,
∴y=2x2+bx+c=2x2﹣4(m+1)x+2m2+4m+1,
∴n=2×(m﹣1)2﹣4(m+1)(m﹣1)+2m2+4m+1=7,
即AM=BN=7,
∵A(m﹣1,n),B(m+3,n),
∴AB=(m+3)﹣(m﹣1)=4,
∴四边形AMNB的周长为是:AM+MN+NB+BA=7+4+7+4=22,
所以答案是:22.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数![]() ,用
,用![]() 表示这三个数中最大数,例如:
表示这三个数中最大数,例如:![]() ,
,![]()
解决问题:
(1)填空:![]() {
{![]() ,
,![]() ,
,![]() }= ,如果
}= ,如果![]() {
{![]() ,
,![]() ,
,![]() }=
}=![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
(2)如果![]() {
{![]() ,
,![]() ,
,![]() }=
}=![]() ,求
,求![]() 的值;
的值;
(3)如图,在同一坐标系中画出了三个一次函数的图象:![]() ,
,![]() 和
和![]()

请观察这三个函数的图象,
①在图中画出![]() {
{![]() ,
,![]() ,
,![]() }对应的图像(加粗);
}对应的图像(加粗);
②![]() {
{![]() ,
,![]() ,
,![]() }的最小值为 .
}的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两种包装盒,大盒比小盒可多装20克某一物品.已知120克这一物品单独装满小盒比单独装满大盒多1盒.
(1)问小盒每个可装这一物品多少克?
(2)现有装满这一物品两种盒子共50个.设小盒有n个,所有盒子所装物品的总量为w克. ①求w关于n的函数解析式,并写出定义域;
②如果小盒所装物品总量与大盒所装物品总量相同,求所有盒子所装物品的总量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形DEF是三角形ABC平移所得,观察图形:(1)点A的对应点是点 ,点B的对应点是点 ,点C的对应点是点 ;(2)线段AD,BE,CF叫做对应点间的连线,这三条线段之间有什么关系呢?
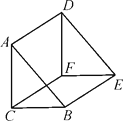
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
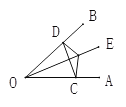
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将连续的奇数![]() ,
,![]() ,
,![]() ,
,![]() ...按图1中的方式排成一个数表,用一个十字框框住
...按图1中的方式排成一个数表,用一个十字框框住![]() 个数,这样框出的任意
个数,这样框出的任意![]() 个数中,四个分支上的数分别用
个数中,四个分支上的数分别用![]() 、
、![]() 、
、![]() 、
、![]() 表示,如图2所示。
表示,如图2所示。

(1)计算:若十字框中间的数为![]() ,则
,则![]() ______________;
______________;
(2)发现:移动十字框,比较![]() 与中间的数
与中间的数![]() .猜想:十字框中
.猜想:十字框中![]() 、
、![]() 、
、![]() 、
、![]() 的和是中间的数
的和是中间的数![]() 的___________________;
的___________________;
(3)验证:用含![]() 的式子表示
的式子表示![]() 、
、![]() 、
、![]() 、
、![]() ,并利用整式运算验证(2)中猜想的正确性;
,并利用整式运算验证(2)中猜想的正确性;
(4)应用:设![]() ,判断
,判断![]() 的值能否等于
的值能否等于![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com