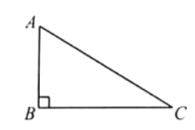
【题目】如图，矩形
中，
，
，
是
边上一点，将
沿
翻折，点
恰好落在对角线
上的点
处，则
的长为________．
【答案】3
【解析】
利用矩形的性质得到BC=AD=8，∠ABC=90°，再根据勾股定理计算出AC=10，接着利用折叠的性质得∠AFE=∠ABE=90°，AF=AB=6，BE=FE，所以CF=4，设BE=x，则EF=x，CE=8-x，利用勾股定理得到x2+42=（8-x）2，解得x=3，即可得出结论.
∵四边形ABCD为矩形，
∴BC=AD=8，∠ABC=90°，
在Rt△ABC中，AC=
，
∵△ABE沿AE翻折，点B恰好落在对角线AC上的点F处，
∴∠AFE=∠ABE=90°，AF=AB=6，BE=FE，
∴CF=10-6=4，
设BE=x，则EF=x，CE=8-x，
在Rt△CEF中，x2+42=（8-x）2，解得x=3，
∴BE=3，
故答案为：3.
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】如图，有一枚质地均匀的正二十面体形状的骰子，其中的1个面标有“1”，2个面标有“2”， 3个面标有“3”，4个面标有“4”，5个面标有“5”，其余的面标有“6”.将这枚骰子掷出后：
（1）数字几朝上的概率最小？
（2）奇数面朝上的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，方格纸中每个小正方形的边长为1cm，平移图中的△ABC，使点B移到点B1的位置．
（1）利用方格和直尺画图
①画出平移后的△A1B1C1
②画出AB边上的中线CD；
③画出BC边上的高AH；
（2）线段A1C1与线段AC的位置关系与数量关系为 ；
（3）△A1B1C1的面积为 cm2；△BCD的面积为 cm2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（一）知识链接
若点M，N在数轴上，且M，N代表的实数分别是a，b，则线段MN的长度可表示为 .
（二）解决问题
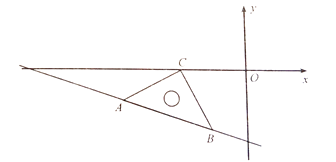
如图，将一个三角板放置在平面直角坐标系中，∠ACB=90°，AC=BC，点B，C的坐标分别为（-2，-4），（-4，0）.
（1）求点A的坐标及直线AB的表达式；
（2）若P是x轴上一点，且S△ABP=6，求点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了预防流感，某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中，室内每立方米空气中含药量y（毫克）与时间x（分钟）成正比例；药物释放完毕后，y与x成反比例，如图所示.根据图中提供的信息，解答下列问题：
（1）写出从药物释放开始，y与x之间的两个函数关系式及相应的自变量取值范围；
（2）据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小东设计的“作矩形”的尺规作图过程，已知：
求作：矩形
作法：如图，
①作线段
的垂直平分线角交于点
；
②连接
并延长，在延长线上截取
③连接
所以四边形即为所求作的矩形
根据小东设计的尺规作图过程
（1）使用直尺和圆规，补全图形：（保留作图痕迹）
（2）完成下边的证明：
证明：
，，
四边形是平行四边形（ ）（填推理的依据）
四边形是矩形（ ）（填推理的依据）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，边长为6的正方形ABCD内部有一点P,BP=4，∠PBC=60°，点Q为正方形边上一动点，且△PBQ是等腰三角形，则符合条件的Q点有__________个.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一元二次方程
，有下列说法：
①若
，则方程必有一个根为1；
②若方程
有两个不相等的实根，则方程必有两个不相等的实根；
③若
是方程的一个根，则一定有
成立；
④若
是一元二次方程的根，则
．
其中正确的有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
