
如图所示,甲、乙、丙三根电线杆垂直于地面,已知甲、乙两根电线杆在地面上的影子.
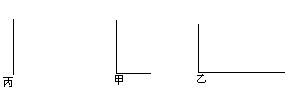
(1)判断投影的类别,并说明理由;
(2)若是中心投影,指出光源的位置,并画出丙电线杆的影子.
|
解: (1)是中心投影,因为分别过甲、乙两根电线杆的顶端和其在地面上的影子的顶端作两直线,这两直线交于点M.由此可知这是中心投影.(2)由(1)知,光源的位置在M点,过M点和两电线杆的顶端作直线交地面于一点,连接这点和丙电线杆的底部便得丙电线杆的影子. 解析:判断投影类别关键是看光线是否平行,若投射光线平行,则是平行投影,若投影变成不平行,则属于中心投影,其中两条投射光线的交点是光源,通过甲、乙两电线杆的顶端和它们的影子的顶端分别作直线,发现这两条投射光线交于一点,因此是中心投影,确定光源的位置便可以作出丙在地面上的影子. 思维延伸:判断投影类别应通过两个不同物体与其影子所得到的光线是否平行来确定.若平行,则为平行投影,若不平行 (即相交),则为中心投影. |


科目:初中数学 来源: 题型:
 4、如图所示,甲、乙、丙、丁、戊五名同学有以下说法:
4、如图所示,甲、乙、丙、丁、戊五名同学有以下说法:查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图所示,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是32cm2,四边形ABCD的面积是20cm2,则甲、乙、丙、丁四个长方形周长的总和为
18、如图所示,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是32cm2,四边形ABCD的面积是20cm2,则甲、乙、丙、丁四个长方形周长的总和为查看答案和解析>>
科目:初中数学 来源: 题型:
 65°.若
65°.若 |
| AB |
 |
| DE |
 |
| GH |
| A、甲=乙=丙 |
| B、甲<乙<丙 |
| C、甲<丙<乙 |
| D、丙<乙<甲 |
查看答案和解析>>
科目:初中数学 来源:2012年河北省石家庄市重点中学中考数学二模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com