
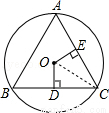
如图,在⊙O中,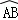 与
与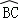 相等,OD⊥BC,OE⊥AC,垂足分别为D、E,且OD=OE,那么△ABC是什么三角形,为什么?
相等,OD⊥BC,OE⊥AC,垂足分别为D、E,且OD=OE,那么△ABC是什么三角形,为什么?

等边三角形
【解析】
试题分析:根据圆心角、弧、弦的关系由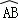 =
=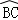 得到AB=BC,再由OD⊥BC,OE⊥AC,根据垂径定理和垂直的定义得到CE=
得到AB=BC,再由OD⊥BC,OE⊥AC,根据垂径定理和垂直的定义得到CE=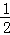 AC,CD=
AC,CD=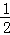 BC,∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC(HL),则CD=CE,于是有BC=AC,则AB=AC=CB,即可得到△ABC为等边三角形.
BC,∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC(HL),则CD=CE,于是有BC=AC,则AB=AC=CB,即可得到△ABC为等边三角形.
【解析】
△ABC为等边三角形.理由如下:
连OC,
∵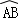 =
=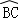 ,
,
∴AB=BC,
∵OD⊥BC,OE⊥AC,
∴CE=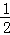 AC,CD=
AC,CD=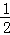 BC,∠ODC=∠OEC=90°
BC,∠ODC=∠OEC=90°
∵在Rt△ODC和Rt△OEC中,
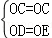 ,
,
∴Rt△ODC≌Rt△OEC(HL)
∴CD=CE,
∴BC=AC,
∴AB=AC=CB,
∴△ABC为等边三角形.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源:2014-2015学年江苏省八年级上学期第二次单元测数学卷(解析版) 题型:填空题
在△ABC中,AD是BC边的中线,AD=3cm,AB=5cm,AC的取值范围为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(云南卷)数学(解析版) 题型:解答题
(9分)(2014•云南)已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,﹣5),点P是直线AC上的一动点.
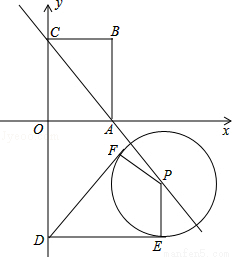
(1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);
(2)当点P沿直线AC移动时,过点D、P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)当点P沿直线AC移动时,以点P为圆心、R(R>0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径长为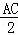 ,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(云南卷)数学(解析版) 题型:选择题
(3分)(2014•云南)据统计,2013年我国用义务教育经费支持了13940000名农民工随迁子女在城市里接受义务教育,这个数字用科学计数法可表示为( )
A.1.394×107 B.13.94×107 C.1.394×106 D.13.94×105
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.3圆心角2(解析版) 题型:解答题
如图,在⊙O中,AD=BC.
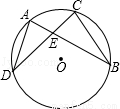
(1)比较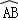 与
与 的长度,并证明你的结论;
的长度,并证明你的结论;
(2)求证:DE=BE.
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.3圆心角2(解析版) 题型:填空题
如下图,弦CD、FE的延长线交于圆外点P,割线PAB经过圆心,请你结合现有图形,添加一个适当的条件: ,使结论∠1=∠2能成立.
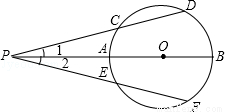
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.3圆心角1(解析版) 题型:?????
下列说法正确的个数为( )
①两条不相交的直线叫平行线;
②三条线段首尾顺次连接的图形叫三角形;
③每条边都相等的多边形叫正多边形;
④相等的圆心角所对的弧相等;
⑤线段是直线的一部分.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.2圆的轴对称性2(解析版) 题型:填空题
如图,⊙O的弦AB⊥AC,AB=AC,OM⊥AB,ON⊥AC,垂足分别为M、N,若AB=2,则⊙O的半径为 .
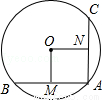
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com