
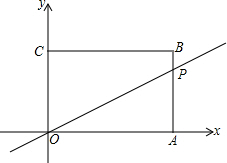
 如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t
如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t 解:如图,∵四边形OABC是矩形,A(4,0),C(0,3),
解:如图,∵四边形OABC是矩形,A(4,0),C(0,3),| OA2+AB2 |
| 42+32 |
| 1 |
| 2 |
| 1 |
| 2 |
| t-3+4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
|
| 3 |
| 2 |
| 3 |
| 2 |


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
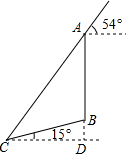 如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).
如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).查看答案和解析>>
科目:初中数学 来源: 题型:
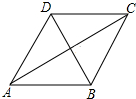 如图,有一张菱形纸片ABCD,AC=8,BD=6.
如图,有一张菱形纸片ABCD,AC=8,BD=6.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com