解:(1)(ab-3a
2)-2b
2-5ab-(a
2-2ab)
原式=ab-3a
2-2b
2-5ab-a
2+2ab
=-4a
2-2b
2-2ab;
(2)原式=

=
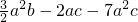
;
(3)原式=xy
2-x
2y,
∵|2x-2|+(y+1)
2=0,
∴2x-2=0,y+1=0
∴x=1,y=-1,
∴原式=1×1-1×(-1)
=2;
(4)根据有理数a、b、c在数轴上的如图所示的对应点知,
a<b<0<c,
∴原式=b-2a-3a-3b-4c+a
=-4a-2b-4c.
分析:(1)、(2)先去括号,再合并同类项;
(3)先化简-2y
3+(3xy
2-x
2y)-2(xy
2-y
3),然后根据非负数的性质求得x、y的值,最后将其代入求值即可;
(3)根据有理数a、b、c在数轴上的对应点,然后先对原式去绝对值并合并同类项.
点评:本题综合考查了数轴、非负数的性质、整式的化简求值等知识点.但都是比较基础的题目,在解答时,只要多一份细心就会很顺利的答对的.

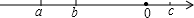 (1)(ab-3a2)-2b2-5ab-(a2-2ab)
(1)(ab-3a2)-2b2-5ab-(a2-2ab)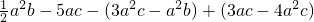

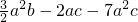 ;
;
