
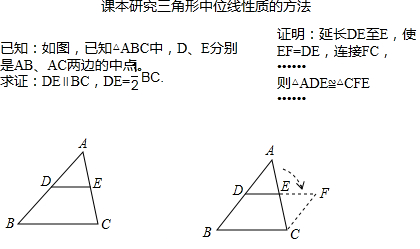
���� ��1�����жϳ���BDF�ա�CDM�����ó�MC=BF����M=��BFM�����жϳ���M=��MAC�ó�AC=MC���ɵó����ۣ�
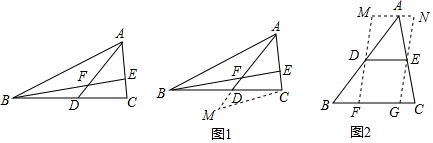
��2�����жϳ��ı���MFGN��ƽ���ı��Σ����жϳ�MN=FG=DE=4�������жϳ�MF��BCʱ���ı���MFGN���ܳ���С��������ֱ�����������AH���ɵó����ۣ�
��� ��1��֤������ͼ1���ӳ�AD����M��ʹMD=FD������MC��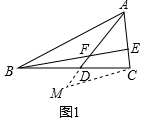
�ڡ�BDF�͡�CDM�У�$\left\{\begin{array}{l}{BD=CD}\\{��BDF=��CDM}\\{DF=DM}\end{array}\right.$��
���BDF�ա�CDM��SAS����
��MC=BF����M=��BFM��
��EA=EF��
���EAF=��EFA��
�ߡ�AFE=��BFM��
���M=��MAC��
��AC=MC��
��BF=AC��
��2���⣺��ͼ2��
��MN��BC��FM��GN��
���ı���MFGN��ƽ���ı��Σ�
��MF=NG��MN=FG��
��DE�ǡ�ABC����λ�ߣ�
��DE=$\frac{1}{2}$BC=4��DE��BC��
��MN=FG=$\frac{1}{2}$BC=4��
���ı���MFGN�ܳ�=2��MF+FG��=2MF+8��
��MF��BCʱ��MF��̣�
�����ı���MFGN���ܳ���С��
����A��AH��BC��H��
��FM=AH
��Rt��ABH�У���B=45�㣬AB=10��
��AH=$\frac{10}{\sqrt{2}}$=5$\sqrt{2}$��
���ı���MFGN���ܳ���СΪ2MF+8=10$\sqrt{2}$+8��
�ʴ�Ϊ��10$\sqrt{2}$+8��
���� ������Ҫ������ȫ�������ε��ж������ʣ������ε���λ�ߣ�ƽ���ı��ε��ж������ʣ�ƽ����ľ��룬�⣨1���ؼ��ǡ�BDF�ա�CDM���⣨2���Ĺؼ����жϳ�MF��BCʱ���ı���MFGN���ܳ���С��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �װ� | 0.1 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
| �Ұ� | 0.8 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
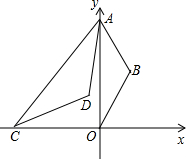 ��ͼ����AΪy����������һ�㣬��OAΪ�ױ���y���Ҳ�������������OAB��ʹ�á�B=120�㣬CΪx����һ�㣬����AC����ACΪ�ױ����Ҳ�������������ACD��ʹ�á�D=120�㣮
��ͼ����AΪy����������һ�㣬��OAΪ�ױ���y���Ҳ�������������OAB��ʹ�á�B=120�㣬CΪx����һ�㣬����AC����ACΪ�ױ����Ҳ�������������ACD��ʹ�á�D=120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������ȵ�ʵ���� | B�� | ����������ȵ�ʵ���� | ||
| C�� | ��ʵ���� | D�� | ��һ��Ϊ0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
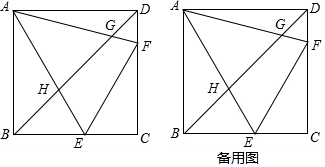 ��ͼ��������ABCD����EAF=45�㣮��BC��CD��E��F����BD��H��G��
��ͼ��������ABCD����EAF=45�㣮��BC��CD��E��F����BD��H��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
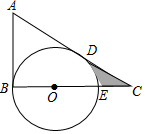 ��ͼ���ڡ�ABC�У���ABC=90�㣬E��BC�ϵ�һ�㣬��BEΪֱ���ġ�O��AC�����ڵ�D����A=60�㣬��O�İ뾶Ϊ2������Ӱ���ֵ����2$\sqrt{3}$-$\frac{2}{3}$�У�������������źͦУ�
��ͼ���ڡ�ABC�У���ABC=90�㣬E��BC�ϵ�һ�㣬��BEΪֱ���ġ�O��AC�����ڵ�D����A=60�㣬��O�İ뾶Ϊ2������Ӱ���ֵ����2$\sqrt{3}$-$\frac{2}{3}$�У�������������źͦУ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com