
| A. | (-5,3) | B. | (-5,-1) | C. | (1,3) | D. | (1,-3) |
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:选择题
| A. | 对全国中学生心理健康现状的调查 | |
| B. | 谋批次汽车的抗重击能力的调查 | |
| C. | 春节联欢会晚会收视率的调查 | |
| D. | 对你所在的班级同学的身高情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
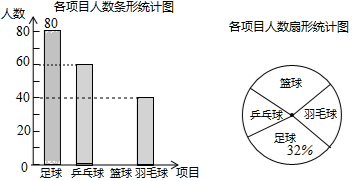
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
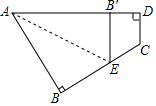 如图所示,一个四边形纸片ABCD,∠D=90°把纸片按如图所示折叠,使点B落在AD上的B′处,AE是折痕.
如图所示,一个四边形纸片ABCD,∠D=90°把纸片按如图所示折叠,使点B落在AD上的B′处,AE是折痕.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com