在平面直角坐标系中,已知函数y1=2x和函数y2=-x+6,不论x取何值,y0都取y1与y2二者之中的较小值.
(1)求y0关于x的函数关系式;
(2)现有二次函数y=x2-8x+c,若函数y0和y都随着x的增大而减小,求自变量x的取值范围;
(3)在(2)的结论下,若函数y0和y的图象有且只有一个公共点,求c的取值范围.
解:(1)联立
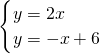
,
解得
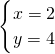
,
所以,y
0=

;
(说明:两个自变量取值范围都含有等号或其中一个含等号均不扣分,都没等号扣1分)
(2)∵对函数y
0,当y
0随x的增大而减小,
∴y
0=-x+6(x≥2),
又∵函数y的对称轴为直线x=4,且a=1>0,
∴当x≤4时,y随x的增大而减小,
∴2≤x≤4;
(3)①若函数y=x
2-8x+c与y
0=-x+6只有一个交点,且交点在2<x<4范围内,
则x
2-8x+c=-x+6,
即x
2-7x+(c-6)=0,
△=73-4c=0,
解得c=18

,
此时x
1=x
2=

,符合2<x<4,
所以,c=18

,
②若函数y=x
2-8x+c与y
0=-x+6有两个交点,其中一个在2≤x≤4范围内,另一个交点在2≤x≤4范围外,
则△=73-4c>0,
解得c<18

,
方法一:对于y
0=-x+6,当x=2时,y
0=4,
当x=4时,y
0=2,
又∵当2≤x≤4时,y随x的增大而减小,
若y=x
2-8x+c与y
0=-x+6在2<x<4内有一个交点,
则当x=2时,y>y
0,当x=4时,y<y
0,
即当x=2时,y≥4;当x=4,时y≤2,
也就是

,
解得16<c<18,
由c<18

,得16<c<18…..…
方法二:联立

消去y得,
x
2-7x+(c-6)=0,
解得x=

,
由函数y=x
2-8x+c与y
0=-x+6的一个交点在2≤x≤4范围内,另一个交点在2≤x≤4范围外,
可得:

或

,
解第一个不等式组,可得

即无解,
解第二个不等式组,可得

即16<c<18,
由c<18

,得16<c<18.
综上所述,c的取值范围是:c=18

或16<c<18.
分析:(1)联立两函数解析式求出交点坐标,然后根据一次函数的增减性解答;
(2)根据一次函数的增减性判断出x≥2,再根据二次函数解析式求出对称轴,然后根据二次函数的增减性可得x≤4,从而得解;
(3)①若函数y=x
2-8x+c与y
0=-x+6只有一个交点,联立两函数解析式整理得到关于x的一元二次方程,利用根的判别式△=0求出c的值,然后求出x的值,若在x的取值范围内,则符合;②若函数y=x
2-8x+c与y
0=-x+6有两个交点,先利用根的判别式求出c的取值范围,方法一:先求出x=2与x=4时的函数值,然后利用一个解在x的范围内,另一个解不在x的范围内列出不等式组求解即可;方法二:联立两函数解析式整理得到关于x的一元二次方程,并求出方程的解,再根据两个解一个在x的范围内,另一个解不在x的范围内列出不等式组求解即可.
点评:本题是二次函数综合题型,主要涉及联立两函数解析式求交点坐标,一次函数与二次函数的增减性,以及交点的个数的讨论求解,(3)难点在于要分只有一个交点且交点横坐标在x的取值范围内,有两个交点,但只有一个交点的横坐标在x的取值范围内,而另一交点在范围外,比较复杂且难度较大.

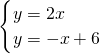 ,
,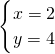 ,
, ;
; ,
, ,符合2<x<4,
,符合2<x<4, ,
, ,
, ,
, ,得16<c<18…..…
,得16<c<18…..… 消去y得,
消去y得, ,
, 或
或 ,
, 即无解,
即无解, 即16<c<18,
即16<c<18, ,得16<c<18.
,得16<c<18. 或16<c<18.
或16<c<18.

 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.