
【题目】如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
A.△CAE∽△BDA
B.![]()
C.BD?CE=4
D.BE=![]() BF
BF
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.

(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
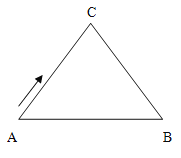
【题目】如图,△ABC中,AC=BC=10 cm,AB=12 cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2 cm,设运动时间为![]() 秒.
秒.
(1)求CD的长;
(2)当![]() 为何值时,△ADP是直角三角形?
为何值时,△ADP是直角三角形?
(3)直接写出:当![]() 为何值时,△ADP是等腰三角形?
为何值时,△ADP是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).
(1)请画出与△OAB关于原点对称的△OCD;(其中A的对称点为C,B的对称点为D)
(2)在(1)的条件下,连接BC、DA,请画出一条直线MN(不与直线AC和坐标轴重合),将四边形ABCD的面积分成相等的两部分,其中M、N分别在AD和BC上,且M、N均为格点,并直接写出直线MN的解析式(写出一个即可).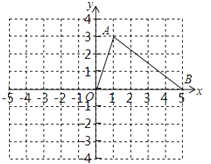
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x、y的多项式(m﹣2)![]() +(n+3)xy2+3xy﹣5.
+(n+3)xy2+3xy﹣5.
(1)若原多项式是五次多项式,求m、n的值;
(2)若原多项式是五次四项式,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数x,y在数轴上对应点如图所示:
![]()
(1)在数轴上表示﹣x,|y|;
(2)试把x,y,0,﹣x,|y|这五个数从小到大用“<”号连接,
(3)化简:|x+y|﹣|y﹣x|+|y|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强电动自行车质量监管,切实保障消费者的合法权益,2015年11月,河南开封市工商局对24个品牌批次的电动自行车进行抽查检验,其中抽查检验的某品牌的电动自行车如图所示,它的大灯M射出的光线MA,MB的与MN的夹角分别为76°和60°,MN⊥地面CD,MN=0.8m,图中的阴影部分表示在夜晚时,灯M所照射的范围.(提示:![]() ≈1.7,sin14°
≈1.7,sin14°![]() , cos14°≈
, cos14°≈![]() , tan14
, tan14![]() )
)
(1)求阴影部分的面积;
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s.小鹏某天晚上以6m/s的速度驾驶该车,在行驶的途中,通过大灯M,他发现在他的正前方有一个小球(即小孩在图中的点A处),小鹏从做出刹车动作到电动自行车停止的刹车距离为1.3m,请判断小鹏当时是否有撞到该小孩?(大灯M与前轮前端间的水平距离为0.3m).
查看答案和解析>>
科目:初中数学 来源: 题型:
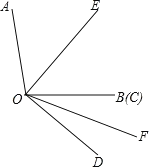
【题目】已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数;
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.
(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
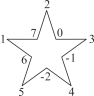
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com