

分析 (1)根据统计图可以得到D占的百分比和C型号种子的发芽数,从而可以将统计图补充完整;
(2)根据统计图可以计算出各种型号种子的发芽率,从而可以解答本题.
解答  解:(1)由扇形统计图可得,
解:(1)由扇形统计图可得,
D占的百分比为:1-35%-20%-20%=25%,
∵C型号种子的发芽率为95%,
∴C型号的种子发芽数为:2000×20%×95%=380,
故补全的图-1,图-2如右图所示,
(2)由题意可得,
A型号的发芽率是:$\frac{630}{2000×35%}$×100%=90%,
B型号的发芽率是:$\frac{370}{2000×20%}$×100%=92.5%,
C型号的发芽率是:95%,
D型号的发芽率是:$\frac{470}{2000×25%}$×100%=94%,
由上可得,发芽率最高的是C型号的种子,
19÷0.1÷95%=200(粒)
即大约需要发芽率最高的种子200粒.
点评 本题考查条形统计图、扇形统计图,解题的关键是明确题意,利用数形结合的思想解答问题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
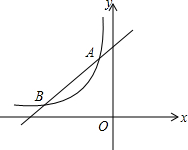 如图,直线y1=k1x+b与反比例函数${y_2}=\frac{k_2}{x}$(x<0)的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的坐标为(-4,m).
如图,直线y1=k1x+b与反比例函数${y_2}=\frac{k_2}{x}$(x<0)的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的坐标为(-4,m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x+1 | B. | y=x2+1 | C. | y=$\sqrt{x+1}$ | D. | y=$\frac{1}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com