
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.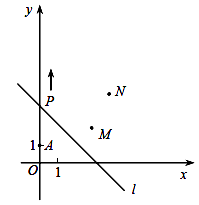
(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
【答案】
(1)解:直线y=-x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,b=1+t.
当t=3时,b=4,
故y=-x+4.
(2)解:当直线y=-x+b过点M(3,2)时,
2=-3+b,
解得:b=5,
5=1+t,
解得t=4.
当直线y=-x+b过点N(4,4)时,
4=-4+b,
解得:b=8,
8=1+t,
解得t=7.
故若点M,N位于l的异侧,t的取值范围是:4<t<7.
(3)解:如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
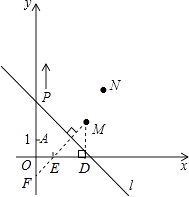
过点M作MD⊥x轴于点D,则OD=3,MD=2.
已知∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,-1).
∵M(3,2),F(0,-1),
∴线段MF中点坐标为( ![]() ,
, ![]() ).
).
直线y=-x+b过点( ![]() ,
, ![]() ),则
),则 ![]() =-
=- ![]() +b,解得:b=2,
+b,解得:b=2,
2=1+t,
解得t=1.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=-x+b过点(2,1),则1=-2+b,解得:b=3,
3=1+t,
解得t=2.
故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上.
【解析】(1)利用直线的平移规律,上加下减,可求出解析式;(2)l令直线y=-x+b过点M、N,求出这两个临界点对应的t值,t的范围就是介于这两个值之间;(3)坐标轴包括x、y轴,分两类,利用轴对称的性质,求出t值.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.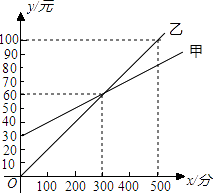
(1)有月租费的收费方式是(填甲或乙),月租费是元;
(2)求出甲、乙两种收费方式中y与自变量x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.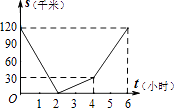
B.
C.
D.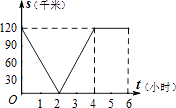
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.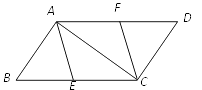
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )
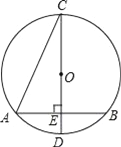
A. 4cm B. 3![]() cm C. 2
cm C. 2![]() cm D. 2
cm D. 2![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,某校进行了宣传动员并公布了相关项目如下:
A——杆身橡筋动力模型;B——直升橡筋动力模型;C——空轿橡筋动力模型.右图为该校报名参加科技比赛的学生人数统计图.
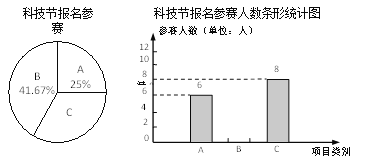
(1)该校报名参加B项目学生人数是 人;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是 °;
(3)为确定参加区科技节的学 生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,请你用学过的数学统计量分析派谁代表学校参赛?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com