
分析 先根据分式的混合运算顺序和法则化简原式,再将x的值代入求解可得.
解答 解:原式=[$\frac{{x}^{2}-4x+3}{x-3}$+$\frac{1}{x-3}$]•[$\frac{(x-1)^{2}}{(x-1)(x-2)}$-$\frac{2}{x-2}$]
=$\frac{(x-2)^{2}}{x-3}$•($\frac{x-1}{x-2}$-$\frac{2}{x-2}$)
=$\frac{(x-2)^{2}}{x-3}$•$\frac{x-3}{x-2}$
=x-2,
当x=4时,
原式=4-2=2.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
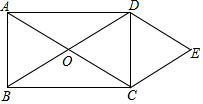 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
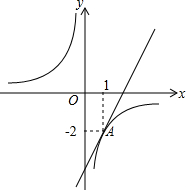 如图,直线y=2x+b与双曲线y=$\frac{k}{x}$(k≠0)只有一个公共点A(1,-2).
如图,直线y=2x+b与双曲线y=$\frac{k}{x}$(k≠0)只有一个公共点A(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
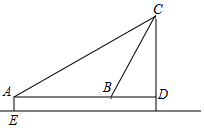 衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图| 部门 | 员工人数 | 每人所创的年利润/万元 |
| A | 5 | 10 |
| B | b | 8 |
| C | c | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
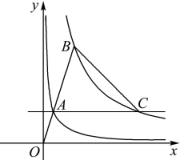 如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.
如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com