
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
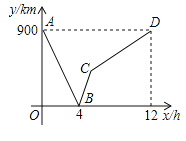
(1)甲、乙两地之间的距离为 千米;图中点B的实际意义是 ;
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
【答案】(1)900,4小时两车相遇.
(2)所以线段BC所表示的y与x之间的函数关系式为:y=225x﹣900(4≤x≤6)
(3)第二列快车比第一列快车晚出发0.75小时
【解析】
试题(1)根据观察图象,可得甲乙两地的距离,根据图象中的点的实际意义即可知道,图中点B的实际意义是:4小时两车相遇.
(2)根据观察图象,可得快车所用的时间,慢车所用的时间,根据路程与时间的关系求得速度,进而求得快车从甲地驶往乙地所用的时间,然后根据待定系数法即可求得函数关系式;
(3)求得第二列快车与慢车相遇所用的时间和此时第一列快车行驶的时间,即可求得第二列快车比第一列快车晚出发的时间.
解:(1)由图象可知,甲、乙两地间的距离是900km;图中点B的实际意义是:4小时两车相遇;
故答案为:900,4小时两车相遇.
(2)慢车速度是:900÷12=75km/h,两车的速度和:900÷4=225km/h
快车速度是:225﹣75=150km/h;
相遇时慢车行驶的路程75×4=300km,
两车相遇后快车到达乙地所用的时间:300÷150=2h,
两车相遇后,2h两车行驶的路程:225×2=450km,
所以,B(4,0),C(6,450),
设线段BC的解析式为y=kx+b,
则![]() ,
,
解得![]() .
.
所以线段BC所表示的y与x之间的函数关系式为:y=225x﹣900(4≤x≤6)
(3)相遇时快车行驶的路程900﹣300=600km,
第二列快车与慢车相遇时行驶的路程:600﹣75×=562,5km,
第二列快车与慢车相遇时所用的时间:562,5÷150=3.75h,
4.5﹣3.75=0.75h.
所以,第二列快车比第一列快车晚出发0.75小时


科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
①画出△ABC向上平移6个单位得到的△A1B1C1;
②以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列因式分解的过程:
(1)x2﹣xy+4x﹣4y
=(x2﹣xy)+(4x﹣4y)(分成两组)
=x(x﹣y)+4(x﹣y)直接提公因式)
=(x﹣y)(x+4)
(2)a2﹣b2﹣c2+2bc
=a2﹣(b2+c2﹣2bc)(分成两组)
=a2﹣(b﹣c)2(直接运用公式)
=(a+b﹣c)(a﹣b+c)
(1)请仿照上述分解因式的方法,把下列各式分解因式:
①![]()
②![]()
(2)请运用上述分解因式的方法,把多项式1+x+x(1+x)+x(1+x)2+…+x(1+x)n分解因式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中(单位长度为![]() ),已知点
),已知点![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若点![]() 是第一象限内一点,且
是第一象限内一点,且![]() 轴,点
轴,点![]() 到
到![]() 轴的距离为4,过点
轴的距离为4,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 从点
从点![]() 处出发,以每秒
处出发,以每秒![]() 的速度沿直线
的速度沿直线![]() 向左移动,点
向左移动,点![]() 从原点
从原点![]() 同时出发,以每秒
同时出发,以每秒![]() 的速度沿
的速度沿![]() 轴向右移动.
轴向右移动.
①经过几秒![]() 平行于
平行于![]() 轴?
轴?
②若某一时刻以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形的面积是
为顶点的四边形的面积是![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
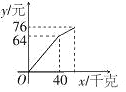
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com