
【题目】一条东西走向的商业街上,依次有书店(记为A)、冷饮店(记为B)、鞋店(记为C),冷饮店位于鞋店西边50m处,鞋店位于书店东边60m处,王平先去书店,然后沿着这条街向东走了30m至D处,接着向西走50m到达E处.
(1)以A为原点、向东为正方向画数轴,在数轴上表示出上述A,B,C,D,E的位置;
(2)若在这条街上建一家超市,使超市与鞋店C分居E点两侧,且到E点的距离相等,问超市在冷饮店的什么方向?距离多远?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
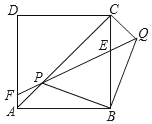
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
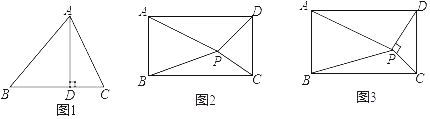
【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=![]() c2,则
c2,则![]() 的值为 (请直接写出结果)
的值为 (请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
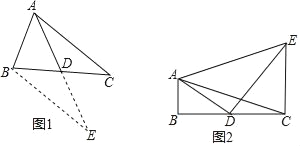
【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在△ABC中,AB=8,AC=6,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,再证明“△ADC≌△EDB”.
(1)探究得出AD的取值范围是_____;
(2)(问题解决)如图2,△ABC中,∠B=90°,AB=2,AD是△ABC的中线,CE⊥BC,CE=4,且∠ADE=90°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
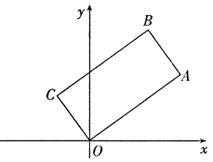
【题目】如图,在矩形![]() 中,
中, ![]() ,顶点
,顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 的坐标为(8,6).
的坐标为(8,6).
(1)顶点![]() 的坐标为( , ),顶点
的坐标为( , ),顶点![]() 的坐标为( , );
的坐标为( , );
(2)现有动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 沿线段
沿线段![]() 向终点
向终点![]() 运动,速度为每秒2个单位,点
运动,速度为每秒2个单位,点![]() 沿折线
沿折线![]() →
→![]() →
→![]() 向终点
向终点![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位.当运动时间为2秒时,以点
个单位.当运动时间为2秒时,以点![]() 、
、![]() 、
、![]() 顶点的三角形是等腰三角形,求
顶点的三角形是等腰三角形,求![]() 的值.
的值.
(3)若矩形![]() 以每秒
以每秒![]() 个单位的速度沿射线
个单位的速度沿射线![]() 下滑,直至顶点
下滑,直至顶点![]() 到达坐标原点时停止下滑.设矩形
到达坐标原点时停止下滑.设矩形![]() 在
在![]() 轴下方部分的面积为
轴下方部分的面积为![]() ,求
,求![]() 关于滑行时间
关于滑行时间![]() 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
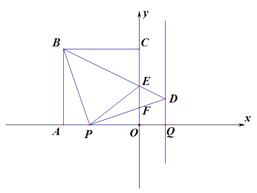
【题目】如图,边长为![]() 正方形OABC的边OA、OC在坐标轴上.在
正方形OABC的边OA、OC在坐标轴上.在![]() 轴上线段
轴上线段![]() (Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为
(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为![]() .连接PB,过P作PB的垂线,过Q作
.连接PB,过P作PB的垂线,过Q作![]() 轴的垂线,两垂线相交于点D.连接BD交
轴的垂线,两垂线相交于点D.连接BD交![]() 轴于点E,连接PD交
轴于点E,连接PD交![]() 轴于点F,连接PE.
轴于点F,连接PE.
(1)求∠PBD的度数.
(2)设△POE的周长为![]() ,探索
,探索![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
(3)令![]() ,当△PBE为等腰三角形时,求△EFD的面积.
,当△PBE为等腰三角形时,求△EFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
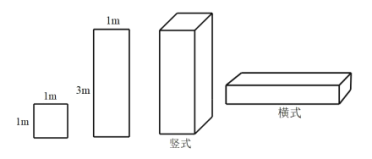
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上O、A两点对应的数为0、10,Q为数轴上一点.
(1)Q为OA线段的中点(即点Q到点O和点A的距离相等),点Q对应的数为 .
(2)数轴上有点 Q,使 Q到O、A的距离之和为20,点Q对应的数为 .
(3)若点Q点表示8,点M以每秒钟5个单位的速度从O点向右运动,点N以每秒钟1个单位的速度从A点向右运动,t秒后有 QM= QN,求时间t的值t= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com