
 如图,根据道路管理规定,直线l的路段上行驶的车辆,限速60千米/时,已知测速站点M距离直线l的距离MN为30米(如图所示),现有一辆汽车匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
如图,根据道路管理规定,直线l的路段上行驶的车辆,限速60千米/时,已知测速站点M距离直线l的距离MN为30米(如图所示),现有一辆汽车匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.分析 (1)已知MN=30m,∠AMN=60°,∠BMN=45°求AB的长度,可以转化为解直角三角形;
(2)求得从A到B的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.
解答 解:(1)在Rt△AMN中,MN=30,∠AMN=60°,
∴AN=MN•tan∠AMN=30$\sqrt{3}$.
在Rt△BMN中,
∵∠BMN=45°,
∴BN=MN=30.
∴AB=AN+BN=(30+30$\sqrt{3}$)米;
(2)∵此车从A点行驶到B点所用时间为6秒,
∴此车的速度为:(30+30$\sqrt{3}$)÷6=5+5$\sqrt{3}$≈13.66,
∵60千米/时≈16.66米/秒,
∴13.66<16.66
∴不会超速.
点评 本题考查了解直角三角形的应用,解题的关键是从题目中抽象出直角三角形,难度不大.


科目:初中数学 来源: 题型:解答题
 如图,某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°,沿山坡AM走到D处测得塔尖B的仰角为30°,已知AC为100米,山坡坡度i=1:3,C、A、E三点在同一直线上.求此人所在位置点D的铅直高度DE.(结果保留根号形式)
如图,某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°,沿山坡AM走到D处测得塔尖B的仰角为30°,已知AC为100米,山坡坡度i=1:3,C、A、E三点在同一直线上.求此人所在位置点D的铅直高度DE.(结果保留根号形式)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
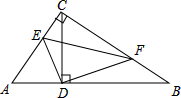 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.
在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com