
【题目】如图, ![]() 的平分线交
的平分线交![]() 的外接圆于点
的外接圆于点![]() ,
, ![]() 的平分线交
的平分线交![]() 于点
于点![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求
,求![]() 外接圆的半径.
外接圆的半径.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:
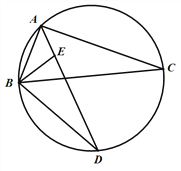
(1)由AD平分∠BAC,BE平分∠ABC,可得∠BAD=∠CAD,∠ABE=∠EBC,结合∠CBD=∠CAD,可得∠CBD=∠BAD;由此结合三角形外角的性质可证得:∠BED=∠EBD,从而可得DE=DB;
(2)连接CD,由∠BAC=90°可得∠BDC=90°;由∠BAD=∠CAD,可得CD=BD=5,从而可得△BDC是等腰直角三角形,再由勾股定理可求得BC的长,从而可得△ABC外接圆的半径.
试题解析:
(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∵∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
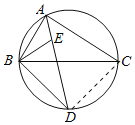
(2)连接CD,如图所示:
由(1)可知:∠BAD=∠CAD,
∴CD=BD=5,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC=![]() ,
,
∴△ABC外接圆的半径![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC .
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(![]() ,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的
,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的![]() ?若存在,请求出点N的坐标;若不存在,请说明理由.
?若存在,请求出点N的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:(1)射线AB与射线BA是同一条射线;(2)两点之间,直线最短;(3)在![]() ,(﹣3)3 , ﹣22 , 0,﹣(﹣2)中,负数的个数有3个;(4)若AP=PB,则点P是线段AB的中点;(5)一条直线的平行线有且只有一条.其中错误的个数为( )
,(﹣3)3 , ﹣22 , 0,﹣(﹣2)中,负数的个数有3个;(4)若AP=PB,则点P是线段AB的中点;(5)一条直线的平行线有且只有一条.其中错误的个数为( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
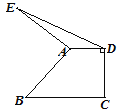
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于 ( )
A.10 B.11 C.12 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.
(1)将图①中的三角尺绕点O顺时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,则∠CON=________;
(2)将图①中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边MN恰好与射线OC平行;在第________秒时,直线ON恰好平分锐角∠AOC(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中是真命题的是( )
A.相等的角是对顶角B.两条直线被第三条直线所截,同位角相等
C.实数与数轴上的点是一一对应的D.垂直于同一条直线的两条直线互相平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com