
 如图,在△ABC中,BC=2,∠A=70°,以BC边为直径作⊙O,分别交AB,AC于点D,E,连接DO,EO,则S扇形OBD+S扇形OEC=$\frac{7}{18}$π.(结果用π表示)
如图,在△ABC中,BC=2,∠A=70°,以BC边为直径作⊙O,分别交AB,AC于点D,E,连接DO,EO,则S扇形OBD+S扇形OEC=$\frac{7}{18}$π.(结果用π表示) 分析 先连接BE,根据圆周角定理可知∠AEB=90°,再由直角三角形的性质求出ABE的度数,由圆周角定理即可得出∠DOE的度数,最后根据∠DOB与∠COE的度数之和,求得S扇形OBD+S扇形OEC的值.
解答 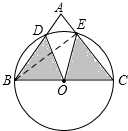 解:连接BE,
解:连接BE,
∵BC是直径,
∴AC⊥BE,
∴∠ABE=90°-∠A=20°,
∴∠DOE=2∠ABE=40°,
∴∠DOB+∠COE=140°,
又∵两个扇形的半径都是1,
∴S扇形OBD+S扇形OEC=$\frac{140×π×{1}^{2}}{360}$=$\frac{7}{18}$π.
故答案为:$\frac{7}{18}$π.
点评 本题主要考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 最低分 | B. | 众数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com