
认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+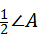 ,理由如下:
,理由如下:
∵BO 和CO分别是∠ABC和∠ACB的角平分线
和CO分别是∠ABC和∠ACB的角平分线
∴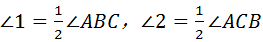
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴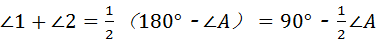
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣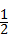 ∠A)
∠A)
=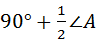 .
.
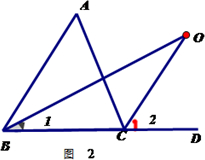
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: .
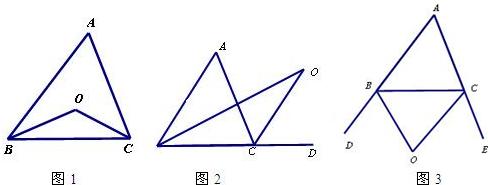
分析:(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠O的关系;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.
解:(1)探究2结论:∠BOC=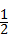 ∠A,
∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=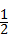 ∠ABC,∠2=
∠ABC,∠2=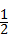 ∠ACD,
∠ACD,
又∵∠ACD是△ABC的一外角,
 ∴∠ACD=∠A+∠ABC,
∴∠ACD=∠A+∠ABC,
∴∠2=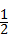 (∠A+∠ABC)=
(∠A+∠ABC)=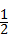 ∠A+∠1,
∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1=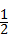 ∠A+∠1﹣∠1=
∠A+∠1﹣∠1=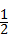 ∠A;
∠A;
(2)探究3:∠OBC=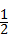 (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB=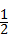 (∠A+∠ABC),
(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣ ∠OCB,
∠OCB,
=180°﹣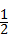 (∠A+∠ACB)﹣
(∠A+∠ACB)﹣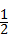 (∠A+∠ABC),
(∠A+∠ABC),
=180°﹣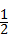 ∠A﹣
∠A﹣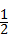 (∠A+∠ABC+∠ACB),
(∠A+∠ABC+∠ACB),
结论∠BOC=90°﹣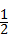 ∠A.
∠A.


科目:初中数学 来源: 题型:
如图,已知ON⊥l,OM⊥l,所以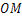 与
与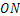 重合,其理由是( )
重合,其理由是( )
A.两点确定一条直线
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点只能作一条垂线
D.垂线段最短
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com