掷两颗骰子得到两个数,注意大数减去小数的差数,回答下列问题并说明理由.
(1)是否有一个差数比其他差数更容易出现?
(2)现有类似骰子的两个正方体六个面上的数字分别为2、3、4、5、6、7,是否有一个差数更容易出现?数字分别为3、4、5、6、7、8呢?并推广之;
(3)若六个面上数字分别为2、4、6、8、10、12,是否有一个差数更容易出现?数字分别是3、6、9、12、15、18呢?并推广之.
解:(1)大数减去小数的差数列表如下:
| | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | | 1 | 2 | 3 | 4 | 5 |
| 2 | | | 1 | 2 | 3 | 4 |
| 3 | | | | 1 | 2 | 3 |
| 4 | | | | | 1 | 2 |
| 5 | | | | | | 1 |
| 6 | | | | | | |
因为1出现的概率是
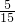
=

,
所以差数1比其他差数更容易出现.
(2)两个正方体六个面上的数字分别为2、3、4、5、6、7时,大数减去小数的差数列表如下:

因为1出现的概率是
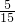
=

,
所以差数1比其他差数更容易出现;
数字分别为3、4、5、6、7、8时,差数1比其他差数更容易出现,可以推广;
(3)数字分别为2、4、6、8、10、12时,大数减去小数的差数列表如下:
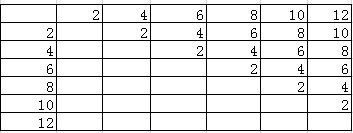
因为2出现的概率是
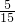
=

,
所以差数2比其他差数更容易出现,
数字分别为3、6、9、12、15、18时,差数3比其他差数更容易出现.
分析:(1)把大数减去小数的差数进行列表,求出每一差数出现的概率,即可求出答案;
(2)根据两个正方体六个面上的数字分别为2、3、4、5、6、7进行列表,即可求出答案;
(3)根据六个面上数字分别为2、4、6、8、10、12进行列表,求出每一差数出现的概率,即可求出答案;
点评:此题考查了列表法求概率,用到的知识点是列表法,解题的关键是根据题意列出图表,求出概率.

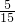 =
= ,
,
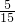 =
= ,
,
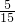 =
= ,
,

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案