
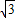 ��������OA�����߶�OA��ԭ��O˳ʱ����ת120°���õ��߶�OB��
��������OA�����߶�OA��ԭ��O˳ʱ����ת120°���õ��߶�OB��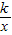 ��x��0����ͼ����һ����Q����Q���������ϵĵ�A���ڵ�M��1��t�������ĶԳƣ������߶�ABΪһֱ�DZߵġ�QABΪֱ��������ʱ����ֱ��д����Ӧ�ķ����������Ľ���ʽ��
��x��0����ͼ����һ����Q����Q���������ϵĵ�A���ڵ�M��1��t�������ĶԳƣ������߶�ABΪһֱ�DZߵġ�QABΪֱ��������ʱ����ֱ��д����Ӧ�ķ����������Ľ���ʽ��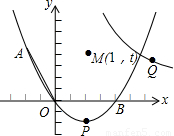
 ����
����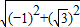 =2��
=2��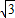 ����B��2��0�����ã�
����B��2��0�����ã�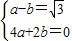 �����
�����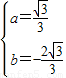
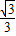 x2-
x2-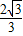 ��
�� ��3����P��x��
��3����P��x��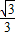 x2-
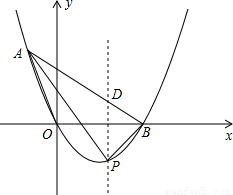
x2-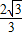 ����0��x��2������P��PD��y�ύ�߶�AB��D��
����0��x��2������P��PD��y�ύ�߶�AB��D��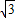 ����B��2��0�����룬�ã�
����B��2��0�����룬�ã�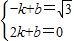 �����
�����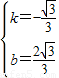
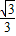 x+
x+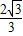 �����D�����꣨x��-
�����D�����꣨x��-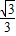 x+
x+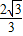 ����
����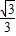 x+
x+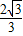 ��-��
��-��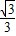 x2-
x2-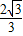 ��=-
��=-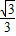 x2+
x2+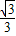 x+
x+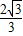 ��
�� ��-
��-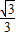 x2+
x2+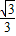 x+
x+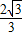 ��×3=-
��×3=-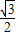 x2+
x2+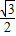 x+
x+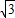 ��
�� ��0��x��2�ķ�Χ�ڣ���˵�x=
��0��x��2�ķ�Χ�ڣ���˵�x= ʱ����PAB�������������ֵΪ
ʱ����PAB�������������ֵΪ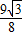 ��
�� ��-
��-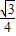 ����
����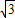 �����ڵ�M��1��t�������ĶԳƣ����Ե�Q�ĺ������Ϊ3��
�����ڵ�M��1��t�������ĶԳƣ����Ե�Q�ĺ������Ϊ3��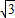 ��
��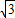 x+b������B��2��0�����ã�b=-2
x+b������B��2��0�����ã�b=-2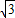 ��
��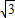 x-2
x-2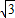 ����x=3ʱ��y=
����x=3ʱ��y=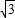 ���� Q��3��
���� Q��3��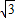 ����
����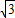 ��
��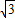 ��
��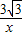 ��y=
��y=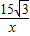 ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ֱ������ϵ�У���P������Ϊ��3��4������OP��ԭ��O��ʱ����ת90��õ��߶�OP�䣮
��ͼ����ֱ������ϵ�У���P������Ϊ��3��4������OP��ԭ��O��ʱ����ת90��õ��߶�OP�䣮 | PP�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2����������ABC������λ��ͼ�Ρ�A1B1C1����A2B2C2��ͬʱ������������������
��2����������ABC������λ��ͼ�Ρ�A1B1C1����A2B2C2��ͬʱ�������������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com