
【题目】如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )

A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4
B.8
C.12
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3x2+3y2﹣5xy,B=2xy﹣3y2+4x2.
(1)化简:2B﹣A;
(2)已知﹣a|x﹣2|b2与![]() aby的同类项,求2B﹣A的值
aby的同类项,求2B﹣A的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-3pq)2;
(2)-x3+(-4x)2x;
(3)(m4m÷m2n)·mn;
(4)(-2)-2-32÷(3.144+π)0;
(5)(a2)3·(a2)4÷(-a2)5;
(6)[-2-3-8-1×(-1)-2]×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB上 一点O,以O为端点画射线OC,作∠AOC的角平分线OD,作∠BOC的角平分线OE;

(1)按要求完成画图;
(2)通过观察、测量你发现∠DOE= °;
(3)补全以下证明过程:
证明:∵OD平分∠AOC(已知)
∴∠DOC= ∠AOC( )
∵OE平分∠BOC(已知)
∴∠EOC= ∠BOC( )
∵∠AOC+∠BOC= °
∴∠DOE=∠DOC+∠EOC= (∠AOC+∠BOC)= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
(1)求证:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圆O的半径及tan∠APB.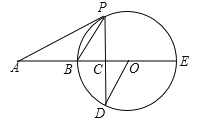
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天放学后,小红步行,小丽骑自行车沿同一条笔直的马路到图书馆看书,图中线段OA、BC分别表示小红、小丽离开学校的路程s(米)与小红所用的时间t(分钟)的函数关系,根据图象解答下列问题:
(1)小丽比小红迟出发 分钟,小红步行的速度是 米/分钟;(直接写出结果)
(2)两人在路上相距不超过200米的时间有多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com