
(1)如图14,矩形ABCD中,AB=5cm,BC=2cm,在AB边上取一点E,(点E与A、B 不重合),连接DE、CE,分矩形ABCD所成的3个三角形都相似.我们把这样的点E叫做矩形ABCD的AB边上的强相似点,在图12的AB边上画出满足要求的强相似点E,并求
不重合),连接DE、CE,分矩形ABCD所成的3个三角形都相似.我们把这样的点E叫做矩形ABCD的AB边上的强相似点,在图12的AB边上画出满足要求的强相似点E,并求 AE的长;(画图工具不限)
AE的长;(画图工具不限)
 |
(2)对于任意一个矩形ABCD,AB边上是否一定存在这样的强相似点E?如果一定存在,请说明理由;如果不一定存在,请举例说明;
(3)在四边形ABCD中,AD∥BC,AD<BC,∠B=90°,当点E是四边形ABCD的AB边上的一个强相似点时.
猜想:AE与BE的数量关系__________________________.
并分别给出理由.
解:(1)画图1,△DAE∽△EBC∽△CE D.
D.
∵△DAE∽△EBC,∴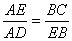
设AE=xcm,则BE=(5-x)cm
即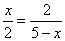
 解得
解得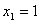 ,
,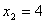
∴AE的长为1cm 或4cm.

(2)对于任意的一个矩形,不一定存在,如正方形.
(答案不惟一,若学生画图说明即可.)
(3)AE与BE的数量关系为:BE=2AE或BE=AE
(注:写出一个关系即可得1分,全对得2分,下面证明共两种情况,每种情况占2分,共4分,具体方法请酌情赋分。)
理由如下:
∵DA∥CB ∴∠A =∠ B=90°
B=90°
第一种情况:如图3,∵点E是梯形ABCD的AB 边上的一个强相似点,
∠A=∠B=∠EDC=90°,∠ADE=∠BCE=∠DCE,
∴△ADE∽△BCE∽△DCE.
所以∠DEA=∠CEB=∠DEC=60°,…说明DE=2AE,CE=2BE,CE=2DE,
即:2BE=2×2AE
所以BE=2AE.



 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米):如果AB的长为x,面积为y,

(1)求面积y与x的函数关系(写出x的取值范围)(8分)
(2)x取何值时,面积最大?面积最大是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
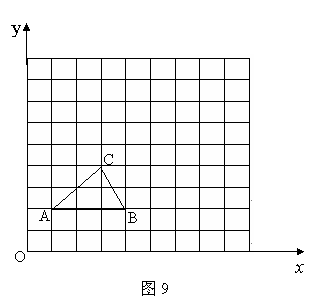
如图,在10×10网格中,每个小方格的边长看做单位1,每个小方格的顶点叫做格点,△ABC的顶点都在格点上.
(1)请在网格中画出△ABC的一个位似图形△A1B1C1,使两个图形以点C为位似中心,且所画图形与△ABC的位似比为2:1;
(2)将△A1B1C1绕着点C1顺时针旋转90°得△A2B2C2,画出图形,并分别写出△A2B2C2三个顶点的坐标.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
王老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
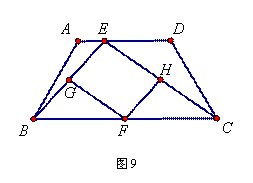
如图9,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)试探索四边形EGFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?并加以证明;
(3)若(2)中的菱形EGFH是正方形,请探索线段EF与线段BC的关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com