
如图, 是△
是△ 的外角
的外角 的平分线,交
的平分线,交 的延长线于
的延长线于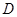 ,延长
,延长 交△
交△ 的外接圆于点
的外接圆于点 ,连结
,连结 ,
, .
.

(1)求证: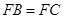 ;
;
(2)求证: ;
;
(3)若 是△
是△ 外接圆的直径,
外接圆的直径,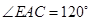 ,
, ,求
,求 的长.
的长.
(1)(2)见解析;(3)
【解析】
试题分析:(1)可通过证角相等来得出边相等,根据ACBF是圆的内接四边形,那么外角∠DAC=∠FBC,那么关键就是证明∠FCB=∠DAC,根据AD平分∠EAC,即∠EAD=∠DAC=∠FAB,我们发现∠FAB和∠FCB正好对应了同一段弧,因此便可得出∠FBC=∠FCB了;
(2)本题实际要证明△FBA和△FDB相似,(1)中已证得∠FAB=∠FCB=∠FBC,又有一个公共角,因此两三角形就相似了;
(3)根据∠EAC=120°可以得到∠DAC=60°,根据AB是△ABC外接圆的直径可以提出AC⊥BC,然后在直角三角形ABC中,有∠BAC的度数,有BC的长,就能求出AC的长,然后在直角三角形ACD中,根据∠ACD=60°,即可用三角函数求出AD.
(1) ,
, ,
,
 .
.
 ,
, ,
,
 ,
,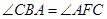 ,
,
 .
.
 ,
,
 ,
,
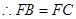 ;
;
(2) ,
, ,
,
 .又
.又 ,
,
 △
△ △
△ ,
,
 ,
,
即 ;
;
(3) 是直径,
是直径, .
.
 ,
,
 ,
,
 .
.
在Rt△ 中,
中, ,
, ,
, .
.
在Rt△ 中,
中, .
.
考点:圆的综合题
点评:本题知识点多,综合性强,在中考中比较常见,在各种题型中均有出现,难度较大,需特别注意.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源:期中题 题型:证明题

 ∠A;
∠A; 查看答案和解析>>
科目:初中数学 来源: 题型:
如图:∠ACD是△ABC的外角,BE平行∠ABC,CE平分∠ACD,且BE、CE交于点E.
求证:(1)∠E=![]() ∠A.
∠A.
(2)若BE、CE是△ABC两外角平线且交于点E,则∠E与∠A又有什么关系?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图:∠ACD是△ABC的外角,BE平行∠ABC,CE平分∠ACD,且BE、CE交于点E.
求证:(1)∠E=![]() ∠A.
∠A.
(2)若BE、CE是△ABC两外角平线且交于点E,则∠E与∠A又有什么关系?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com