
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
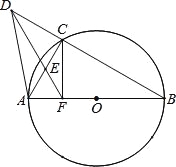
【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)由AB是⊙O直径,得到∠ACB=90°,由于△AEF为等边三角形,得到∠CAB=∠EFA=60°,根据三角形的外角的性质即可得到结论;
(2)过点A作AM⊥DF于点M,设AF=2a,根据等边三角形的性质得到FM=EM=a,AM=![]() a,在根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到AE=EF=AF=CE=2a,推出∠ECF=∠EFC,根据三角形的内角和即可得到结论.
a,在根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到AE=EF=AF=CE=2a,推出∠ECF=∠EFC,根据三角形的内角和即可得到结论.
试题解析:(1)∵AB是⊙O直径,
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°,
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
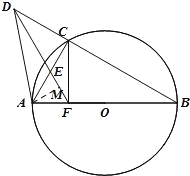
(2)过点A作AM⊥DF于点M,设AF=2a,
∵△AEF是等边三角形,∴FM=EM=a,AM=![]() a,
a,
在Rt△DAM中,AD=![]() AF=
AF=![]() a,AM=
a,AM=![]() a,
a,
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=4a,
∵AE=EF=AF=2a,
∴CE=AC﹣AE=2a,
∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列说法:
·(1)若 ![]() =﹣1,则a<0
=﹣1,则a<0
·(2)若a,b互为相反数,则an与bn也互为相反数
·(3)a2+3的值中最小的值为3
·(4)若x<0,y>0,则|xy﹣y|=﹣(xy﹣y)
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)16÷(﹣2)3﹣(﹣ ![]() )×(﹣4);
)×(﹣4);
(2)|﹣1 ![]() |×(0.5﹣
|×(0.5﹣ ![]() )÷1
)÷1 ![]() ;
;
(3)[1﹣(1﹣0.5× ![]() )]×[2﹣(﹣3)2]
)]×[2﹣(﹣3)2]
(4)﹣14﹣(1﹣0.5)× ![]() ×[10﹣(﹣2)2]﹣(﹣1)3 .
×[10﹣(﹣2)2]﹣(﹣1)3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x﹣2y,B=﹣x﹣4y+1
(1)求3(A+B)﹣2(2A﹣B)的值;(结果用x、y表示)
(2)当 ![]() 与(y﹣1)2互为相反数时,求(1)中代数式的值.
与(y﹣1)2互为相反数时,求(1)中代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
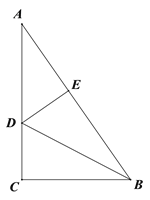
【题目】如图,Rt△ABC中,∠ACB=90°,D为AC上一动点(不与点A、C重合),过D作DE⊥AB于E.
(1)当BD平分∠ABC时
①若AC=8,BC=6,求线段AE的长度;
②在①的条件下,求△ADB的面积;
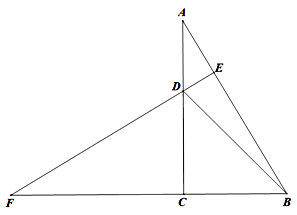
(2)延长BC、ED相交于点F,若CD=CB,∠CDF=60°,求∠DBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=![]() ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥![]() .正确的是( ).
.正确的是( ).
A.①② B.③④ C.①②③ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com