
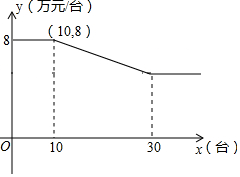
 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系如图所示.分析 (1)由“总利润=单台利润×销售数量”结合图象即可得出结论;
(2)设y与x之间的函数关系式为y=kx+b,由函数图象找出点的坐标,再利用待定系数法即可求出结论;
(3)再将x=15可以求得相应的y的值,从而可以求出当x=15时,公司所获得的总利润.
解答 解:(1)当x=10时,公司销售机器人的总利润为10×(10-8)=20(万元).
故答案为:20.
(2)设y与x之间的函数关系式为y=kx+b,
∵函数图象过点(10,8),(30,6),
∴有$\left\{\begin{array}{l}{8=10k+b}\\{6=30k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=9}\end{array}\right.$.
∴当10≤x≤30时,y与x的函数关系式为y=-$\frac{1}{10}$x+9;
(3)把x=15代入y=-$\frac{1}{10}$x+9得y=7.5,
∴总利润为:(10-7.5)×15=37.5(万元),
即当x=15时,公司所获得的总利润为37.5万元.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com