
 ,
,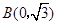 ,
,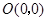 ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到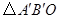 .
.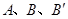 ,求该抛物线解析式;
,求该抛物线解析式; 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点 的坐标及面积的最大值.
的坐标及面积的最大值.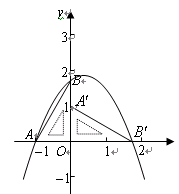


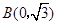 ,将坐标代入上解析式得:
,将坐标代入上解析式得: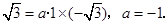


 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,
 则
则
 点坐标满足
点坐标满足


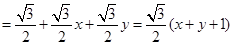

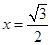 时,
时, 最大.
最大. .即当动点
.即当动点 的坐标为
的坐标为 时,
时, 最大,最大面积为
最大,最大面积为

 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,
 且
且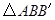 的面积为定值,
的面积为定值,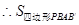 最大时
最大时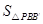 必须最大.
必须最大. 长度为定值,∴
长度为定值,∴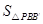 最大时点
最大时点 到
到 的距离最大.
的距离最大. 向上平移到与抛物线有唯一交点时,
向上平移到与抛物线有唯一交点时, 到
到 的距离最大.
的距离最大. 平行的直线
平行的直线 的解析式为
的解析式为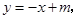



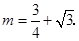 此时直线
此时直线 的解析式为:
的解析式为: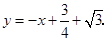
 解得
解得
 与抛物线唯一交点坐标为
与抛物线唯一交点坐标为
 与
与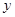 轴交于
轴交于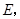 则
则
 作
作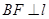 于
于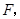 在
在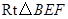 中,
中,
 作
作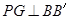 于
于 则
则 到
到 的距离
的距离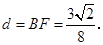
 的面积最大.
的面积最大. 的最大值=
的最大值=
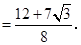
 三点的坐标根据待定系数法即可求出解析式;
三点的坐标根据待定系数法即可求出解析式;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为 ,则点D的横坐标最大值为( )
,则点D的横坐标最大值为( )
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (x>0),若该车某次的刹车距离为5 m,则开始刹车时的速度为( )
(x>0),若该车某次的刹车距离为5 m,则开始刹车时的速度为( )| A.40 m/s | B.20 m/s |
| C.10 m/s | D.5 m/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com