
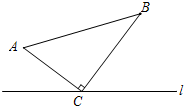
 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8. 分析 易证∠MEC=∠CFN,∠MCE=∠CNF.只需MC=NC,就可得到△MEC与△CFN全等,然后只需根据点M和点N不同位置进行分类讨论即可解决问题.
解答 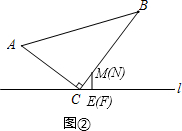
 解:①当0≤t<4时,点M在AC上,点N在BC上,如图①,
解:①当0≤t<4时,点M在AC上,点N在BC上,如图①,
此时有AM=2t,BN=3t,AC=8,BC=15.
当MC=NC即8-2t=15-3t,
解得t=7,不合题意舍去;
②当4≤t<5时,点M在BC上,点N也在BC上,如图②,
若MC=NC,则点M与点N重合,即2t-8=15-3t,
解得t=$\frac{23}{5}$;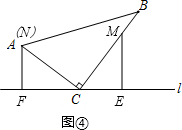
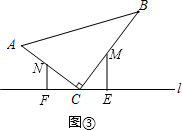 ③当5≤t<$\frac{23}{3}$时,点M在BC上,点N在AC上,如图③,
③当5≤t<$\frac{23}{3}$时,点M在BC上,点N在AC上,如图③,
当MC=NC即2t-8=3t-15,
解得t=7;
④当$\frac{23}{3}$≤t<$\frac{23}{2}$时,点N停在点A处,点M在BC上,如图④,
当MC=NC即2t-8=8,
解得t=8;
综上所述:当t等于$\frac{23}{5}$或7或8秒时,以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等.
故答案为:$\frac{23}{5}$或7或8.
点评 本题主要考查了全等三角形的判定以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.


科目:初中数学 来源: 题型:选择题
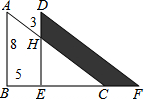 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7,24,25 | B. | 1.5,2,2.5 | C. | $\frac{5}{4}$,1,$\frac{3}{4}$ | D. | 40,50,60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
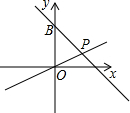 如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).
如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com