
【题目】抛物线y=x2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(-1,0).
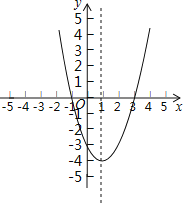
(1)写出B点的坐标 ;
(2)求抛物线的函数解析式;
(3)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(4)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
【答案】(1)B(3,0);(2)y=x22x3;(3)P(6,21)或(6,45);(4)![]() .
.
【解析】
(1)函数的对称轴为:x=1,点A(1,0),则点B(3,0);
(2)用两点式求解即可;
(3)△POC的面积是△BOC的面积的2倍,则|xP|=2OB=6,即可求解;
(4)易得直线BC的表达式,设出点M(x,x3),则可得MD=x3(x22x3)=x2+3x,然后求二次函数的最值即可.
解:(1)函数的对称轴为:x=1,点A(1,0),则点B(3,0),
故答案为(3,0);
(2)函数的表达式为:y=(x+1)(x3)=x22x3;
(3)△POC的面积是△BOC的面积的2倍,则|xP|=2OB=6,
当x=6时,y=36123=21,
当x=6时,y=36+123=45,
故点P(6,21)或(6,45);
(4)∵B(3,0),C(0,-3),
易得直线BC的表达式为:y=x3,
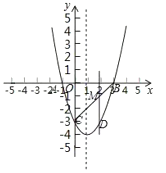
设点M(x,x3),则点D(x,x22x3),
∴MD=x3(x22x3)=x2+3x,
∵1<0,
∴MD有最大值,
∴当x=![]() 时,其最大值为:
时,其最大值为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
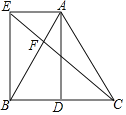
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若BE=2![]() ,AE=2,求EF的长.
,AE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为( )

A. ![]() B.
B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了这样一道题目:“当![]() 时,求多项式
时,求多项式![]() 的值”.解完这道题后,张恒同学指出:“
的值”.解完这道题后,张恒同学指出:“![]() 是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.
是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.
(1)请你说明正确的理由;
(2)受此启发,老师又出示了一道题目,“无论![]() 取任何值,多项式
取任何值,多项式![]() 的值都不变,求系数
的值都不变,求系数![]() 、
、![]() 的值”.请你解决这个问题.
的值”.请你解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个点从数轴上的原点开始,先向右移动1个单位长度,再向左移动2个单位长度,再向右移动3个单位长度,再向左移动4个单位长度,……,移动2019次后,该点所对应的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,正方形
为坐标原点,正方形![]() 与长方形
与长方形![]() 的位置如图所示,点
的位置如图所示,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() ,
,![]() 在
在![]() 轴的负半轴上(点
轴的负半轴上(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 的坐标为
的坐标为![]() ,
,![]() ,实数
,实数![]() ,
,![]() 的值满足
的值满足![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)长方形![]() 以每秒1个单位长度的速度向右平移
以每秒1个单位长度的速度向右平移![]() (
(![]() )秒得到矩形
)秒得到矩形![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别为点
分别为点![]() ,
,![]() ,
,![]() ,
,![]() 平移后的对应点,设矩形
平移后的对应点,设矩形![]() 与正方形
与正方形![]() 重合部分的面积为
重合部分的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并直接写出相应的
,并直接写出相应的![]() 的范围;
的范围;
(3)在(2)的条件下,在长方形![]() 出发运动的同时,点
出发运动的同时,点![]() 从点
从点![]() 出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即
出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即![]() ),连接
),连接![]() ,
,![]() ,当三角形
,当三角形![]() 的面积为15时,求
的面积为15时,求![]() 时相应的
时相应的![]() 值,并直接写出此时刻
值,并直接写出此时刻![]() 值及点
值及点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com