
下图,已知抛物线y=x2+bx+c的图像与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
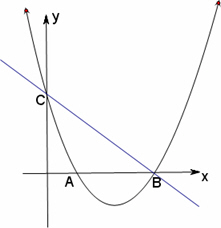
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图像上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图像上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.
∵抛物线y=x2+bx+c与x轴的一个交点为B(5,0),与y轴交于点C(0,5),
∴将B(5,0),C(0,5)代入y=x2+bx+c,
解得:b=-6,c=5.
∴二次函数解析式为:y=x2-6x+5.
设直线BC的解析式为:y=kx+5.
将B(5,0)代入直线BC解析式y=kx+5.
解得:k=-1.
∴直线BC的解析式为:y=-x+5.如图①.设M(x,y),则
NM=-x+5-(x2-6x+5).
NM=-x2+5x.
NM=-(x-)2+.
∴NM的最大值为.

如图②由第2问易得S2=5,∴S1=6S2=30.
BC=,BC所在直线的解析式为:y=-x+5,
∠CBO=45°,
∵S2=30.∴平行四边形CBPQ中BC边上的高为=.
过点C作CD⊥PQ与PQ所在直线相交于点D,
PD交y轴于点E,CD=,∴CE=6,
∵平行四边形CBPQ的边PQ所在直线,在直线BC的两侧可能各有一条,但点P在x轴下方,
∴PQ的解析式为y=-x-1.
∵点P同时在抛物线和直线PQ上,
∴x2-6x+5=-x-1.解得x1=2,x2=3,
∴P1(2,-3),P2(3,-4).


科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:013
已知抛物线y=![]() (x-4)2-3的部分图象(如下图所示),图象再次与x轴相交时的坐标是
(x-4)2-3的部分图象(如下图所示),图象再次与x轴相交时的坐标是

A.(5,0)
B.(6,0)
C.(7,0)
D.(8,0)
查看答案和解析>>
科目:初中数学 来源:2007年江苏地区数学中考动态型试题-新人教 题型:044
已知抛物线y=-x2-2kx+3k2(k>0)交x轴于A、B两点,交y轴于点C,以AB为直径的⊙E交y轴于点D、F(如下图),且DF=4,G是劣弧![]() 上的动点(不与点A、D重合),直线CG交x轴于点P.
上的动点(不与点A、D重合),直线CG交x轴于点P.
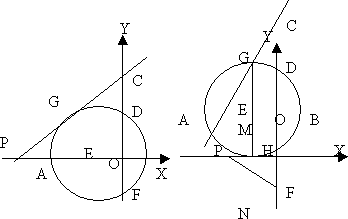
求抛物线的解析式;
当直线CG是⊙E的切线时,求tan∠PCO的值.
当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2009年浙江省湖州市中考数学试题 题型:044
已知抛物线y=x2-2x+a(a<0)与y轴相交于点A,顶点为M.直线![]() 分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.

(1)填空:试用含a的代数式分别表示点M与N的坐标,则M( , ),N( , );
(2)如下图,将△NAC沿y轴翻折,若点N的对应点![]() 恰好落在抛物线上,
恰好落在抛物线上,![]() 与x轴交于点D,连结CD,求a的值和四边形ADCN的面积;
与x轴交于点D,连结CD,求a的值和四边形ADCN的面积;

(3)在抛物线y=x2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源:2006年湖南省郴州市课改实验区初中毕业学业考试试卷数学 题型:059
已知抛物线y=ax2+bx+c经过P(![]() ,3),E
,3),E![]() 及原点O(0,0).
及原点O(0,0).
(1)求抛物线的解析式.
(2)过P点作平行于x轴的直线PC交y轴于C点,在抛物线对称轴右侧且位于直线PC下方的抛物线上,任取一点Q,过点Q作直线QA平行于y轴交x轴于A点,交直线PC于B点,直线QA与直线PC及两坐标轴围成矩形OABC(如下图).是否存在点Q,使得△OPC与△PQB相似?若存在,求出Q点的坐标;若不存在,请说明理由.
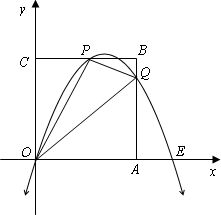
(3)如果符合(2)中的Q点在x轴的上方,连结OQ,矩形OABC内的四个三角形△OPC,△PQB,△OQP,△OQA之间存在怎样的关系?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com