
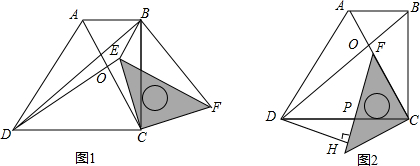
分析 (1)相等,证DE与BF所在的三角形全等即可;
(2)易得∠BEF=90°,那么可得到△BEF各边的比值进而求解;
(3)根据△CFP∽△CDO,利用相似三角形的性质解答.
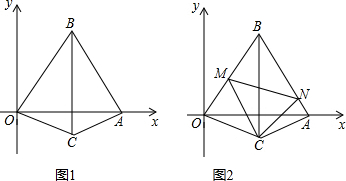
解答 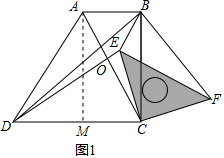 解:(1)如图1,当三角板旋转到图1的位置时,DE=BF,
解:(1)如图1,当三角板旋转到图1的位置时,DE=BF,
∵∠ECB+∠BCF=90°,∠DCE+∠ECB=90°,
∴∠DCE=∠BCF.
∵∠BCD=90°,AB∥CD
∴∠ABC=90°,∠BAC=∠ACD,
∵BC=2,AB=1,
∴tan∠BAC=2,
∵tan∠ADC=2,
∴∠BAC=∠ADC,
∴∠ACD=∠ADC,
∴AD=AC,
作AM⊥CD于点M,
∴CD=2MC=2AB=2,
∴CD=BC.
∵EC=CF,
∴△DCE≌△BCF.
∴DE=BF.
(2)如图2,∵∠BEC=135°,∠FEC=45°,
∴∠BEF=90°.
∵BE:CE=1:2,
∴BE:EF=1:2$\sqrt{2}$.
∴sin∠BFE=BE:BF=$\frac{1}{3}$.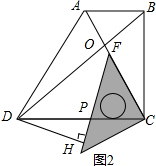
(3)∵△CFP∽△CDO,
CF:CD=CP:CO=PF:DO
AC=$\sqrt{5}$,
AO:CO=1:2,CO=$\frac{2\sqrt{5}}{3}$,
CF=$\frac{2\sqrt{5}}{3}$-$\frac{\sqrt{5}}{6}$=$\frac{\sqrt{5}}{2}$,
$\frac{\sqrt{5}}{2}$:2=CP:$\frac{2\sqrt{5}}{3}$,
CP=$\frac{5}{6}$,
∵DB=2$\sqrt{2}$,BO:DO=1:2,
∴DO=$\frac{4\sqrt{2}}{3}$,
∴PF=$\frac{\sqrt{10}}{3}$,PE=$\sqrt{2}$×$\frac{\sqrt{5}}{2}$-$\frac{\sqrt{10}}{3}$=$\frac{\sqrt{10}}{6}$,即PE=$\frac{\sqrt{10}}{6}$.
点评 此题考查了几何变换综合题.此题涉及到了旋转的性质,等腰直角三角形的性质以及矩形的性质等知识,综合性很强,难度适中,解题的关键是注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
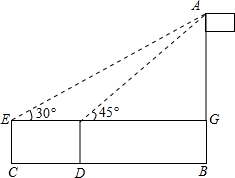 如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)
如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )
如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减少 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
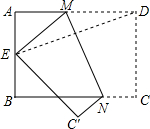 如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
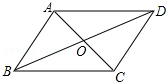 如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )| A. | AB=DC,AD=BC | B. | AB∥DC,AO=BO | C. | AB=DC,∠B=∠D | D. | AB∥DC,∠B=∠D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com