
����Ŀ����ͼ1����ABC�У�AC��BC����ACB��90������PΪAB��һ�㣨����A��B����BD��ֱ��CP��D��AE��ֱ��CP��E����FΪAB���е㣬����DF��
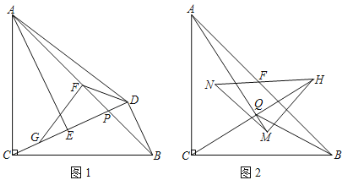
��1��������ACE�Ƶ�F��ʱ����ת�� ���ȣ�����������180���������� ���غϣ����FDE���� ������
��2��ȡCE���е�G������AD��FG����֤��AD��2FG��
��3����ͼ2��AB��8������ֱ����MNH��б��NH���е�ҲΪ��F��ֱ��AM��ֱ��CH���ڵ�Q������BQ������MNH�Ƶ�F��תһ��ʱ����ֱ��д��BQ����ȡֵ��Χ��
���𰸡���1��90��CBD��45����2������������3��2![]() -2
-2![]() ��BQ��2
��BQ��2![]() +2
+2![]()
��������
(1)�ɵ���ֱ�������ε����ʿɵ�CF=AF=BF��CF��BF������AAS����֤��ACE�ա�CBD���������ACE�Ƶ�F��ʱ����ת90�Ⱥ���CBD�غϣ��ɵ�CE=DB��EF=DF����֤��CFE�ա�BFD���ɵá�CFE=��BFD����֤��EFD=90��������⣻
(2)ȡBD�е�H������FH�����е㶨�����������λ�߶����ɵ�CG=![]() CE=
CE=![]() BD=BH��AD��FH��AD=2FH������SAS����֤��CFG�ա�BFH���ɵ�GF=FH���ɵ�AD=2FG��
BD=BH��AD��FH��AD=2FH������SAS����֤��CFG�ա�BFH���ɵ�GF=FH���ɵ�AD=2FG��
(3)��ͼ2������CF��MF����ȫ�������ε����ʿ����AQC=90�����ɵõ�Q����ACΪֱ����Բ���˶���������⣮
(1)��ͼ1������CF��EF��

��AC=BC����ACB=90������FΪAB���е㣬
��CF=AF=BF��CF��BF��
��AE��CD��BD��CD��
���AEC=��CDB=��ACB=90����
���ACE+��CAE=90������ACE+��DCB=90����
���CAE=��DCB����AC=BC����AEC=��CDB=90����
���ACE�ա�CBD(AAS)
�������ACE�Ƶ�F��ʱ����ת90�Ⱥ���CBD�غϣ�
��CE=DB��EF=DF����CF=BF��
���CFE�ա�BFD(SSS)
���CFE=��BFD���ҡ�CFE+��EFB=90����
���BFD+��EFB=90����
���EFD=90������EF=DF��
���FDE=45����
�ʴ�Ϊ��90��CBD��45��
(2)��ͼ1��ȡBD�е�H������FH��
�ߵ�G��CE�е㣬��H��BD�е㣬��F��AB�е㣬��CE=BD��
��CG=![]() CE=
CE=![]() BD=BH��AD��FH��AD=2FH��
BD=BH��AD��FH��AD=2FH��
�ߡ�CFE�ա�BFD��
���FCG=��FBH����CG=BH��CF=BF��
���CFG�ա�BFH(SAS)
��GF=FH��
��AD=2FG��
(3)��ͼ2������CF��MF��

��AC=BC����ACB=90������F��AB�е㣬AB=8��
��AF=CF=BF=4��CF��AB��AC=BC=4![]() ��
��
��MN=MH����NMH=90������F��NH�е㣬
��NF=FH=FM��MF��NH��
���MFH=��AFC=90����
���AFM=��CFH����AF=CF��FH=FM��
���AFM�ա�CFH(SAS)
���FAM=��FCH��
�ߡ�FAM+��CAM+��ACF=90����
���CAM+��ACF+��FCH=90����
���AQC=90����
���Q����ACΪֱ����Բ���˶���
�൱��Q��BO���ӳ�����ʱ��BQ�����Q���߶�BO��ʱ��BQ��С��
ȡAC�е�O������BO��
��CO=2![]() ��
��
��BO=![]() =
=![]() =2
=2![]() ��
��
��BQ����ȡֵ��ΧΪ![]()


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y1��x2+bx+c��ֱ��y2��2x+m�ཻ��A��1��4����B����1��n�����㣮
��1����y1��y2�Ľ���ʽ��
��2��ֱ��д��y1��y2����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ���һö���ؼ��Σ�������˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض���������ÿö�ƽ���x����ÿö������y������������ã�������
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�ÿ��С�����εı߳�Ϊ1������ABC�������������ߵĽ����ϣ��Ķ���A��C������ֱ�ΪA����3��5����C��0��3����
��1�������������ڵ�ƽ���ڻ���ƽ��ֱ������ϵ����д����B�����꣮
��2������ABC����ԭ��˳ʱ����ת90��á�A1B1C1��������A1B1C1��
��3����ֱ��y��1�ϴ���һ��P��ʹPA+PC��ֵ��С����ֱ��д����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��������ABCD������AB��AD���У���DE���O�����ڵ�E����AB��7��DO��5����DE�ij���Ϊ_____��
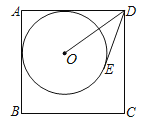
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
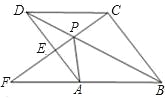
����Ŀ����ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD��E����BA���ӳ��ߵ�F���ʣ�
��1��ͼ����APD���ĸ�������ȫ�ȣ���˵�����ɣ�
��2����֤����APE�ס�FPA��
��3�����룺�߶�PC��PE��PF֮�����ʲô��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
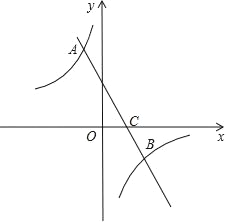
����Ŀ����ͼ��ֱ��y=kx+b��k��0����˫����y=![]() ��m��0�����ڵ�A����
��m��0�����ڵ�A����![]() ��2����B��n����1����
��2����B��n����1����
��1����ֱ����˫���ߵĽ���ʽ��
��2����P��x���ϣ����S��ABP=3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �е�ͼ��M��N���������¶��壺�����PΪͼ��M������һ�㣬��QΪͼ��N������һ�㣬��ô���߶�PQ���ȵ���СֵΪͼ��M��N������������������ d��M��N������ͼ��M��N������������С�ڻ����1�����ͼ��M��N��Ϊ���ɼ�ͼ������
�е�ͼ��M��N���������¶��壺�����PΪͼ��M������һ�㣬��QΪͼ��N������һ�㣬��ô���߶�PQ���ȵ���СֵΪͼ��M��N������������������ d��M��N������ͼ��M��N������������С�ڻ����1�����ͼ��M��N��Ϊ���ɼ�ͼ������
��1������O�İ뾶Ϊ2ʱ��
�������A��0��1����B��3��4������ôd��A����O��=_______,d��B����O��= ________��
�����ֱ��![]() ���O��Ϊ���ɼ�ͼ��������b��ȡֵ��Χ��
���O��Ϊ���ɼ�ͼ��������b��ȡֵ��Χ��
��2����G��Բ��G��![]() ���ϣ��뾶Ϊ1��ֱ��
���ϣ��뾶Ϊ1��ֱ��![]() ��x�ύ�ڵ�C����y�ύ�ڵ�D�������G�͡�CDO��Ϊ���ɼ�ͼ������ֱ��д��Բ��G�ĺ�����m��ȡֵ��Χ��
��x�ύ�ڵ�C����y�ύ�ڵ�D�������G�͡�CDO��Ϊ���ɼ�ͼ������ֱ��д��Բ��G�ĺ�����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĶ���Ϊ![]() ���ҹ���
���ҹ���![]() .ֱ��
.ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() .
.
��1����������ߵĽ���ʽ��
��2�����߶�![]() Ϊֱ����Բ������
Ϊֱ����Բ������![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com