考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)如图,作辅助线;证明CF=2CD;证明△BDC∽△CAF,得到
=,根据CF=2CD,即可解决问题.
(2)如图,证明△ACF∽△DCE,列出比例式求出CE=5,此为解题的关键性结论;证明AB:BC=3:5,借助勾股定理即可解决问题.
解答: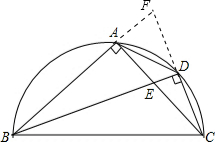
(1)证明:如图,延长CD,交BA的延长线于点F;
∵D为
中点,
∴
=,AD=CD,∠ACD=∠DAC;
∵BC为直径,
∴∠FAC=∠BDC=90°,
∴∠DAF=∠F,AD=DF;
∴CD=DF,CF=2CD;
∵∠FAD=∠BCD,
∴∠F=∠BCD;而∠FAC=∠BDC,
∴△BDC∽△CAF,
∴
=,而CF=2CD,
∴AC•BC=2BD•CD.
(2)解:设CE=λ;则AC=3+λ,CF=2CD=4
;
∵∠CAF=∠EDC,∠ECD=∠DCE,
∴△ACF∽△DCE,
∴
=,
=,
整理得:λ
2+3λ-40=0,
解得:λ=5或-8(舍去);
∵D为
中点,AB
∴∠ABE=∠CBE,即BE平分∠ABC,
∴
==,设AB=3μ,则BC=5μ;
由勾股定理得:(3μ)
2+8
2=(5μ)
2,
解得:μ=2,
∴AB=6,BC=10.
点评:该题主要考查了圆周角定理及其推论、相似三角形的判定及其性质、勾股定理等几何知识点的应用问题;对综合的分析问题解决问题的能力提出了较高的要求.

 已知:D为
已知:D为
 (1)证明:如图,延长CD,交BA的延长线于点F;
(1)证明:如图,延长CD,交BA的延长线于点F;





 阅读快车系列答案
阅读快车系列答案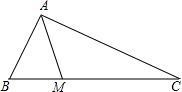 在Rt△ABC中,∠BAC=90°,AB=3,M为边长BC上的点,连接AM,如图,如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是
在Rt△ABC中,∠BAC=90°,AB=3,M为边长BC上的点,连接AM,如图,如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是